题目内容
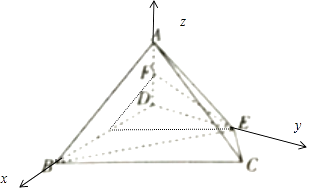
【题目】如图,在四棱锥A﹣BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE. 
(1)若F是AD的中点,求证:EF∥平面ABC;
(2)若AD=DE,求BE与平面ACE所成角的正弦值.
【答案】
(1)证明:取DB中点G,连结EG、FG.
∵F是AD的中点,∴FG∥AB.
∵BD=2CE,∴BG=CE.
∵∠DBC=∠BCE
∴E、G到直线BC的距离相等,则BG∥CB,
∵EG∩FG=G
∴面EGF∥平面ABC,则EF∥平面ABC.
(2)解:以点D为原点,建立如图所示的直角坐标系D﹣xyz,设EC=1,则DB=2,取BC中点C,则EG∥BC,∴BC=3,
∵AD=DE,则A(0,0, ![]() ),E(0,
),E(0, ![]() ,0),B(2,0,0),C(
,0),B(2,0,0),C( ![]() ,
, ![]() ,0).
,0).
![]() ,
, ![]() .
.
设平面ACE的法向量 ![]() ,
,
![]() =
= ![]() x+
x+ ![]() y=0
y=0
令y=1,则 ![]() ,|cos
,|cos ![]() |=
|= ![]() .
.
∴BE与平面ACE所成角的正弦值为: ![]()
【解析】(1)取DB中点G,连结EG、FG.证面EGF∥平面ABC,即可得EF∥平面ABC.(2)以点D为原点,建立如图所示的直角坐标系D﹣xyz,则A(0,0, ![]() ),E(0,
),E(0, ![]() ,0),B(2,0,0),C(
,0),B(2,0,0),C( ![]() ,
, ![]() ,0).求出平面ACE的法向量即可
,0).求出平面ACE的法向量即可
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则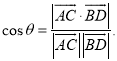 .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案【题目】某地区2009年至2015年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
附:回归直线的斜率和截距的最小二乘估计公式分别为:  .
. ![]() .
.
参考数据:(﹣3)×(﹣1.4)+(﹣2)×(﹣1)+(﹣1)×(﹣0.7)+1×0.5+2×0.9+3×1.6=14.
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2009年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.

