题目内容
【题目】已知椭圆![]() 的左、右焦点分别为F1,F2,离心率
的左、右焦点分别为F1,F2,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)求椭圆的标准方程;
(2)已知直线l1,l2过右焦点F2,且它们的斜率乘积为﹣1,设l1,l2分别与椭圆交于点A,B和C,D.①求AB+CD的值;②设AB的中点M,CD的中点为N,求△OMN面积的最大值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(Ⅰ)由离心率e=![]() ,短轴长为2.可得a,b,即可写出方程;(2)设出直线
,短轴长为2.可得a,b,即可写出方程;(2)设出直线![]() :
:![]() 与椭圆联立,求出
与椭圆联立,求出![]() ,同理
,同理![]() ,
,![]() 求出中点坐标M,N,再利用MN两点确定的直线恒过定点和面积公式即可求出.
求出中点坐标M,N,再利用MN两点确定的直线恒过定点和面积公式即可求出.
(Ⅰ)由题意得2b=2,∴b=1,
∵![]() ,a2=b2+c2,∴a=
,a2=b2+c2,∴a=![]() ,c=1,
,c=1,
∴椭圆的方程为![]() .
.
(2)由题意知k![]() 0,右焦点
0,右焦点![]() 设
设![]() :
:![]()
![]()
![]()
![]() 设A(
设A(![]() )B(
)B(![]() )
)
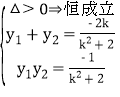
![]()
因为l1,l2的斜率乘积为﹣1,所以![]()
![]() 所以
所以![]() =
= ![]() +
+![]() =3
=3![]()
过定点![]() 可通过特殊情形猜想,若有定点,则在x 轴上.
可通过特殊情形猜想,若有定点,则在x 轴上.
在k≠0,k≠±1的情况下,设直线l![]() 的方程为:x=ky+1,
的方程为:x=ky+1,
直线l![]() 的方程为:
的方程为:![]() ,
,
由(2)得,y![]() =
= ![]() ,
,
故![]() ,即M(
,即M(![]() ,
,![]() ),
),
则N(![]() ,
, ![]() )….(12分)
)….(12分)
可得直线MN的方程: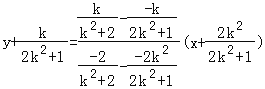 ,
,
即![]() ,则
,则![]()
![]() ,即
,即
y=![]()
故直线MN过定点![]() (或令y=0,即得x=
(或令y=0,即得x=![]() )
)
易验证当k=0,k=±1时,结论仍成立.
综上,直线MN过定点![]()
所以S![]() =
=![]()
![]() =
= ![]()
所以面积最大![]()

练习册系列答案
相关题目