题目内容
【题目】将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
A.33B.56C.64D.78
【答案】B
【解析】
记分隔边的条数为![]() ,首先将方格表按图分成三个区域,, 分别染成三种颜色, 粗线上均为分隔边,将方格表的行从上至下依次记为
,首先将方格表按图分成三个区域,, 分别染成三种颜色, 粗线上均为分隔边,将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,行
,行![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,列
,列![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,三种颜色分别记为
,三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含色方格的行数与列数之和,定义当
为含色方格的行数与列数之和,定义当![]() 行含
行含![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,类似的定义
,类似的定义![]() ,计算得到
,计算得到![]() ,再证明
,再证明![]() ,再证明对任意
,再证明对任意![]() 均有
均有![]() ,
,![]() ,最后求出分隔边条数的最小值.
,最后求出分隔边条数的最小值.
记分隔边的条数为![]() ,首先将方格表按图分成三个区域,如图:
,首先将方格表按图分成三个区域,如图:
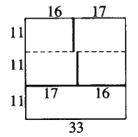
分别染成三种颜色,粗线上均为分隔边,此时共有56条分隔边,则![]() ,
,
其次证明:![]() ,
,
将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,
,
行![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,列
,列![]() 中方格出现的颜色为
中方格出现的颜色为![]() ,
,
三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含色方格的行数与列数之和,
为含色方格的行数与列数之和,
定义当![]() 行含
行含![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,
,
类似的定义![]() ,
,
所以![]()
![]() ,
,
由于染![]() 色的格的行有
色的格的行有![]() 个,列有
个,列有![]() 个,则
个,则![]() 色的方格一定在这
色的方格一定在这![]() 行和
行和![]() 列的交叉方格中,从而
列的交叉方格中,从而![]() ,
,
所以![]()
![]() 所以①,
所以①,
由于在行![]() 中有
中有![]() 种颜色的方格,于是至少有
种颜色的方格,于是至少有![]() 条分隔边,
条分隔边,
类似地,在列![]() 中至少有
中至少有![]() 条分隔边,
条分隔边,
则![]()
![]() ②
②
![]() ③,
③,
下面分两种情况讨论:
1、有一行或一列所有方格同色,不妨设为![]() 色,则方格表的33列中均含有
色,则方格表的33列中均含有![]() 色的方格,又
色的方格,又![]() 色的方格有363个,
色的方格有363个,
故至少有![]() 行含有
行含有![]() 色的方格,于是
色的方格,于是![]() ④,
④,
由①③④得![]() ;
;
2、没有一行也没有一列所有方格同色,对任意![]() 均有
均有![]() ,
,![]() ,
,
从而由②可得![]() ;
;
综上所述,分隔边条数的最小值为56.
故选:B

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目