题目内容
【题目】如图,点![]() 在以
在以![]() 为直径的圆
为直径的圆![]() 上,
上, ![]() 垂直于圆
垂直于圆![]() 所在的平面,
所在的平面, ![]() 为
为![]() 的重心.
的重心.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)要证平面![]() 平面
平面![]() ,只需要证得
,只需要证得![]() 平面
平面![]() 即可,有条件可得
即可,有条件可得![]() ,
, ![]() ;
;
(2)以点![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,利用平面的法向量求余弦值即可.
,利用平面的法向量求余弦值即可.
试题解析:
(1)如图,延长![]() 交
交![]() 于
于![]() ,
,
∵![]() 为
为![]() 的重心,∴
的重心,∴![]() 为
为![]() 的中点,
的中点,
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 是圆
是圆![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)如图,以点![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
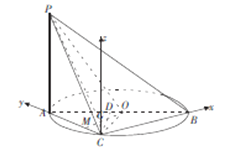
则 ,
,
则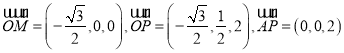 .
.
平面![]() 即为平面
即为平面![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则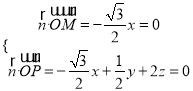 ,令
,令![]() ,得
,得![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,
,
由等面积法可得![]() ,
,
∴![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为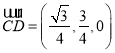 ,
,
设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,
,
则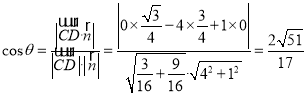 .
.
即平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
【题目】某种产品的以往各年的宣传费用支出![]() (万元)与销售量
(万元)与销售量![]() (万件)之间有如下对应数据
(万件)之间有如下对应数据
| 2 | 4 | 5 | 6 | 8 |
| 4 | 3 | 6 | 7 | 8 |
(1)试求回归直线方程;
(2)设该产品的单件售价与单件生产成本的差为![]() (元),若
(元),若![]() 与销售量
与销售量![]() (万件)的函数关系是
(万件)的函数关系是![]() ,试估计宣传费用支出
,试估计宣传费用支出![]() 为多少万元时,销售该产品的利润最大?(注:销售利润=销售额-生产成本-宣传费用)
为多少万元时,销售该产品的利润最大?(注:销售利润=销售额-生产成本-宣传费用)
(参考数据与公式: ![]() ,
, ![]() ,
, 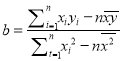 )
)


