题目内容
【题目】已知函数f(x)=2x+2ax+b , 且f(1)= ![]() 、f(2)=
、f(2)= ![]() .
.
(1)求a、b的值;
(2)判断f(x)的奇偶性并证明;
(3)先判断并证明函数f(x)在[0,+∞)上的单调性,然后求f(x)的值域.
【答案】
(1)解:由 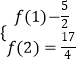 得
得 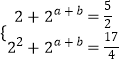
解得 ![]()
(2)解:∵f(x)=2x+2﹣x,f(x)的定义域为R,
由f(﹣x)=2﹣x+2x=f(x),
所以f(x)为偶函数
(3)解:f(x)在[0,+∞)上为增函数.证明如下:
设x1<x2,且x1,x2∈[0,+∞)
![]() =
= ![]() =
= ![]()
因为x1<x2且x1,x2∈[0,+∞)
所以 ![]() ,
, ![]()
所以f(x1)﹣f(x2)<0
所以f(x)在[0,+∞)上为增函数.
∴f(x)≥f(0)=2
f(x)的值域为[2,+∞)
【解析】(1)由f(1)= ![]() 、f(2)=
、f(2)= ![]() 列方程组,解这个指数方程组即可得a、b的值;(2)先求函数的解析式,在求函数的定义域,最后利用函数奇偶性的定义证明函数的奇偶性;(3)利用函数单调性的定义,通过设变量,作差比较函数值的大小证明函数的单调性,利用函数的单调性求函数的值域即可
列方程组,解这个指数方程组即可得a、b的值;(2)先求函数的解析式,在求函数的定义域,最后利用函数奇偶性的定义证明函数的奇偶性;(3)利用函数单调性的定义,通过设变量,作差比较函数值的大小证明函数的单调性,利用函数的单调性求函数的值域即可
【考点精析】掌握函数的值域和函数单调性的判断方法是解答本题的根本,需要知道求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.

【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
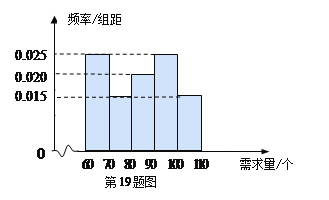
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成頻率分布直方图:
的值,并完成頻率分布直方图:
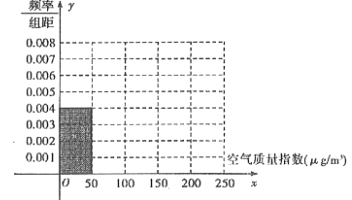
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,从中任意选取
天,从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.