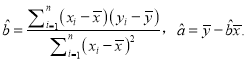题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,求出最大的整数
的图象的下方?若存在,求出最大的整数![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(参考数据: ![]() )
)
【答案】(1)所求切线的方程为![]() (2)存在实数
(2)存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() .
.
【解析】【试题分析】(1)依据题设先求出切点坐标,再对函数求导,进而求出在切点处的导函数值即为切线的斜率,然后运用点斜式求出切线方程;(2)先依据题设建立不等式![]() ,进而将问题转化为即
,进而将问题转化为即![]() 对
对![]() 恒成立。然后构造函数
恒成立。然后构造函数![]() ,再求导数
,再求导数![]() , 令
, 令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
, ![]() ,
,
且![]() 的图象在
的图象在![]() 上连续,所以存在
上连续,所以存在![]() ,使得
,使得![]() ,即
,即![]() ,最后判定当
,最后判定当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,
单调递增,
则![]() 取到最小值
取到最小值![]()
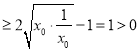 ,
,
所以![]() ,即
,即![]() 在区间
在区间![]() 内单调递增. 所以
内单调递增. 所以![]() ,即存在实数
,即存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() 。
。
解:(1)因为![]() ,所以
,所以![]() ,则所求切线的斜率为
,则所求切线的斜率为![]() .
.
又![]() ,故所求切线的方程为
,故所求切线的方程为![]() .
.
(2)假设存在实数![]() 满足题意,则不等式
满足题意,则不等式![]() 对
对![]() 恒成立.
恒成立.
即![]() 对
对![]() 恒成立
恒成立
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
, ![]() ,/span>
,/span>
且![]() 的图象在
的图象在![]() 上连续,所以存在
上连续,所以存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
则![]() ,
,
所以当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,
单调递增,
则![]() 取到最小值
取到最小值![]()
 ,
,
所以![]() ,即
,即![]() 在区间
在区间![]() 内单调递增.
内单调递增.
所以![]() ,
,
所以存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: