题目内容
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样统计,先将800人按001,002,003,…,800进行编号.
(Ⅰ)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号:(下面摘取了第7行至第9行)

(Ⅱ)抽的100人的数学与地理的水平测试成绩如下表:

成绩优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求![]() 的值.
的值.
(Ⅲ)将![]() ,
, ![]() 的
的![]() 表示成有序数对
表示成有序数对![]() ,求“地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对
,求“地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对![]() 的概率.
的概率.
【答案】(Ⅰ)785,667,199.(Ⅱ)![]() ,
, ![]() (Ⅲ)
(Ⅲ)![]()
【解析】试题分析:(I)按系统抽样的方法可知,编号为![]() .(II)根据频率计算公式,可得
.(II)根据频率计算公式,可得![]() ,根据样本总数列方程可求得
,根据样本总数列方程可求得![]() .(III)根据
.(III)根据![]() ,通过列举可得基本事件总数有
,通过列举可得基本事件总数有![]() 种,其中符合题意的有
种,其中符合题意的有![]() 种,故概率为
种,故概率为![]() .
.
试题解析:
(Ⅰ)依题意,最先检测的3个人的编号依次为785,667,199.
(Ⅱ)由![]() ,得
,得![]() ,
,
∵![]() ,∴
,∴![]() .
.
(Ⅲ)由题意,知![]() ,且
,且![]() ,
, ![]() .
.
故满足条件的![]() 有:
有: ![]()
![]() 共14组.
共14组.
其中数学成绩为优秀的人数比及格的人数少有: ![]() 共6组.
共6组.
∴数学成绩为优秀的人数比及格的人数少的概率为![]() .
.

 小学课时特训系列答案
小学课时特训系列答案【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
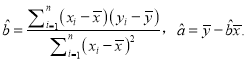
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成頻率分布直方图:
的值,并完成頻率分布直方图:
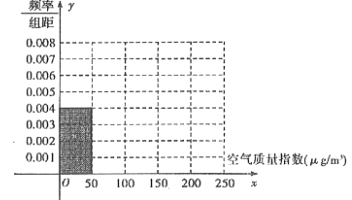
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,从中任意选取
天,从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
