题目内容
【题目】已知双曲线![]() 以
以![]() 为焦点,且过点
为焦点,且过点![]()
(1)求双曲线![]() 与其渐近线的方程
与其渐近线的方程
(2)若斜率为1的直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程
的方程
【答案】(1)双曲线C的方程为![]() ; 渐近线方程为
; 渐近线方程为![]() .(2)l方程为
.(2)l方程为![]() .
.
【解析】
(1)设出双曲线C方程,利用已知条件求出c,a,解得b,即可求出双曲线方程与渐近线的方程;
(2)设直线l的方程为y=x+t,将其代入方程![]() ,通过△>0,求出t的范围,设A(x1,y1),B(x2,y2),利用韦达定理,通过x1x2+y1y2=0,求解t即可得到直线方程.
,通过△>0,求出t的范围,设A(x1,y1),B(x2,y2),利用韦达定理,通过x1x2+y1y2=0,求解t即可得到直线方程.
(1)设双曲线C的方程为![]() ,半焦距为c,
,半焦距为c,
则c=2,![]() ,a=1,
,a=1,
所以b2=c2﹣a2=3,
故双曲线C的方程为![]() .
.
双曲线C的渐近线方程为![]() .
.
(2)设直线l的方程为y=x+t,将其代入方程![]() ,
,
可得2x2﹣2tx﹣t2﹣3=0(*)
△=4t2+8(t2+3)=12t2+24>0,若设A(x1,y1),B(x2,y2),
则x1,x2是方程(*)的两个根,所以![]() ,
,
又由![]() ,可知x1x2+y1y2=0,
,可知x1x2+y1y2=0,
即x1x2+(x1+t)(x2+t)=0,可得![]() ,
,
故﹣(t2+3)+t2+t2=0,解得![]() ,
,
所以直线l方程为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销量y(元) | 88 | 78 | 85 | 75 | 82 | 66 |
(1)分别以三家连锁店的平均售价与平均销量为散点,如A店对应的散点为![]() ,求出售价与销量的回归直线方程
,求出售价与销量的回归直线方程![]() ;
;
(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附: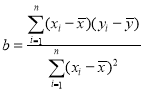 ,
,![]() .
.
【题目】一次考试中,五名学生的数学、物理成绩如下表所示:
学生 | A1 | A2 | A3 | A4 | A5 |
数学(x分) | 89 | 91 | 93 | 95 | 97 |
物理(y分) | 87 | 89 | 89 | 92 | 93 |
(1)要从5名学生中选2人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据线性回归方程![]() .
.