题目内容
如图,已知正方体 中,E是棱
中,E是棱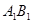 的中点,则异面直线
的中点,则异面直线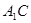 与AE所成角的余弦值是________.
与AE所成角的余弦值是________.
 中,E是棱
中,E是棱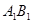 的中点,则异面直线
的中点,则异面直线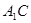 与AE所成角的余弦值是________.
与AE所成角的余弦值是________.

解:建立空间直角坐标系设正方体的边长为1,以A为坐标原点,则利用向量的数量积的夹角公式可以求解得到其向量夹角的余弦值为


练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
题目内容
 中,E是棱
中,E是棱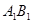 的中点,则异面直线
的中点,则异面直线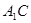 与AE所成角的余弦值是________.
与AE所成角的余弦值是________.



 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案