题目内容
如图,四棱锥S-ABCD中,SD 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD DC,
DC,
AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC 平面SBC .
平面SBC .
(Ⅰ)证明:SE=2EB;
(Ⅱ)求二面角A-DE-C的大小 .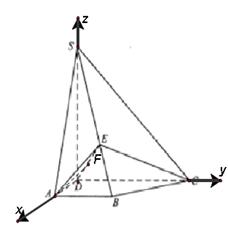
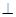 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD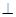 DC,
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
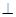 平面SBC .
平面SBC .(Ⅰ)证明:SE=2EB;
(Ⅱ)求二面角A-DE-C的大小 .

(1)见解析;(2)120°.
本试题主要考查了立体几何中的面面垂直和二面角的求解运算。
解:(Ⅰ)连接BD,取DC的中点G,连接BG,
由此知DG=GC=BG=1,即△ABC为直角三角形,故BC⊥BD.
又SD⊥平面ABCD,故BC⊥SD,
所以,BC⊥平面BDS,BC⊥DE.
作BK⊥EC,K为垂足,因平面EDC⊥平面SBC,
故BK⊥平面EDC,BK⊥DE,DE与平面SBC内的两条相交直线BK、BC都垂直,
DE⊥平面SBC,DE⊥EC,DE⊥SD.
SB2=" SD2+DB2" =" 6," DE=SD DB /SB =
DB /SB = 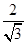 ,
,
EB2=" DB2-DE2" =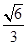 ,SE=SB-EB=
,SE=SB-EB=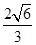 所以SE=2EB
所以SE=2EB
(2) 由SA=" SD2+AD2" =" 5" ,AB=1,SE=2EB,AB⊥SA,知
AE=" (1" /3 SA)2+(2 /3 AB)2 =1,又AD=1.
故△ADE为等腰三角形.
取ED中点F,连接AF,则AF⊥DE,AF2=" AD2-DF2" =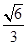 .
.
连接FG,则FG∥EC,FG⊥DE.
所以,∠AFG是二面角A-DE-C的平面角.
连接AG,AG=" 2" ,FG2=" DG2-DF2" =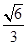 ,
,
cos∠AFG="(AF2+FG2-AG2" )/2?AF?FG ="-1" /2 ,
所以,二面角A-DE-C的大小为120°
解:(Ⅰ)连接BD,取DC的中点G,连接BG,
由此知DG=GC=BG=1,即△ABC为直角三角形,故BC⊥BD.
又SD⊥平面ABCD,故BC⊥SD,
所以,BC⊥平面BDS,BC⊥DE.
作BK⊥EC,K为垂足,因平面EDC⊥平面SBC,
故BK⊥平面EDC,BK⊥DE,DE与平面SBC内的两条相交直线BK、BC都垂直,
DE⊥平面SBC,DE⊥EC,DE⊥SD.
SB2=" SD2+DB2" =" 6," DE=SD
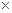 DB /SB =
DB /SB = 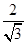 ,
, EB2=" DB2-DE2" =
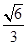 ,SE=SB-EB=
,SE=SB-EB=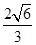 所以SE=2EB
所以SE=2EB(2) 由SA=" SD2+AD2" =" 5" ,AB=1,SE=2EB,AB⊥SA,知
AE=" (1" /3 SA)2+(2 /3 AB)2 =1,又AD=1.
故△ADE为等腰三角形.
取ED中点F,连接AF,则AF⊥DE,AF2=" AD2-DF2" =
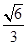 .
.连接FG,则FG∥EC,FG⊥DE.
所以,∠AFG是二面角A-DE-C的平面角.
连接AG,AG=" 2" ,FG2=" DG2-DF2" =
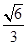 ,
,cos∠AFG="(AF2+FG2-AG2" )/2?AF?FG ="-1" /2 ,
所以,二面角A-DE-C的大小为120°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,底面正方形
中,底面正方形 的边长为1,侧棱长为2,则异面直线
的边长为1,侧棱长为2,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )



 中,E是棱
中,E是棱 的中点,则异面直线
的中点,则异面直线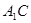 与AE所成角的余弦值是________.
与AE所成角的余弦值是________.





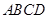 -
- 中,
中, 为
为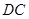 的中点,则
的中点,则 与
与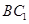 所在直线所成角的余弦值等于 ( ) ( )
所在直线所成角的余弦值等于 ( ) ( )




 中,如图E、F分别是
中,如图E、F分别是  ,CD的中点,
,CD的中点, 平面ADE;
平面ADE; .
. 
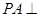 平面
平面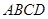 ,四边形
,四边形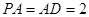 ,点
,点 、
、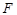 、
、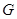 分别为线段
分别为线段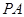 、
、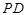 和
和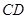 的中点.
的中点.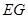 与
与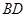 所成角的余弦值;
所成角的余弦值;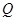 ,使得点
,使得点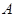 到平面
到平面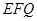 的距离恰为
的距离恰为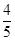 ?若存在,求出线段
?若存在,求出线段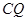 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.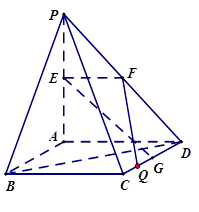
 的底面
的底面 是直角梯形,
是直角梯形, ,
,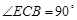 ,
,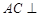 平面
平面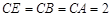 ,
,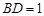 .
.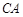 与平面
与平面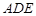 所成角的正弦值;
所成角的正弦值;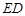 上是否存在一点
上是否存在一点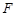 ,使得异面直线
,使得异面直线 与
与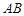 所成角余 弦值等
所成角余 弦值等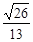 ?若存在,试确定点
?若存在,试确定点