题目内容
7.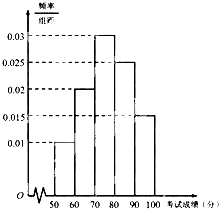 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].(1)试估计全市学生参加汉字听写考试的平均成绩;
(2)如果从参加本次考试的同学中随机选取1名同学,求这名同学考试成绩在80分以上的概率.
分析 (1)根据频率分布直方图,累加各组的组中值与频率的乘积,可得平均成绩;
(2)累积考试成绩在80(分)以上各级的频率,可得这名同学考试成绩在80分以上的概率;
解答 解:(1)估计全市学生参加汉字听写考试的平均成绩为:
0.1×55+0.2×65+0.3×75+0.25×85+0.15×95=76.5;
(2)设被抽到的这名同学考试成绩在80(分)以上为事件A.
P(A)=0.025×10+0.015×10=0.4;
∴被抽到的这名同学考试成绩在80(分)以上的概率为0.4;
点评 本题考查的知识点是利用频率分布直方图估算数据的平均数和概率,难度不大,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
19.直线$\left\{\begin{array}{l}{x=sinθ+tsin15°}\\{y=cosθ-tsin15°}\end{array}\right.$(t为参数,θ是常数)的倾斜角是( )
| A. | 45° | B. | 75° | C. | 105° | D. | 135° |
17.曲线y=x3-3x2+a在点P(1,-1)处的切线方程为( )
| A. | y=3x-4 | B. | y=-4x-1 | C. | y=-3x+2 | D. | y=4x-7 |
 如图所示,公园内有一块边长为2a的等边△ABC形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图所示,公园内有一块边长为2a的等边△ABC形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.