题目内容
17.曲线y=x3-3x2+a在点P(1,-1)处的切线方程为( )| A. | y=3x-4 | B. | y=-4x-1 | C. | y=-3x+2 | D. | y=4x-7 |
分析 求出函数的导数,求得切线的斜率,由点斜式方程,可得切线的方程.
解答 解:函数f(x)的导数为3x2-6x,
切线的斜率为3-6=-3,
即有切线的方程为y+1=-3(x-1),
即为y=-3x+2.
故选C.
点评 本题考查导数的运用:求切线的方程,考查直线方程的求法,考查运算能力,属于基础题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
5.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点(x,y)落在直线y=-x+5上的概率为( )
| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{4}$ |
2.曲线y=$\frac{1}{3}{x^3}$-2在点$(-1,-\frac{7}{3})$处的切线的倾斜角为( )
| A. | 30° | B. | 45° | C. | 135° | D. | -45° |
9.下列判断正确的是( )
| A. | 函数$f(x)=\frac{{{x^2}-x}}{x-1}$是奇函数 | |
| B. | 函数$f(x)=(1-x)\sqrt{\frac{1+x}{1-x}}$是偶函数 | |
| C. | 函数$y=\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$是偶函数 | |
| D. | 函数$y=\frac{{\sqrt{9-{x^2}}}}{{|{x+4}|+|{x+3}|}}$的图象关于y轴对称 |
6.已知x>y>0,下列各式正确的是( )
| A. | $\frac{x+y}{2}$>x>$\sqrt{xy}$>y | B. | x>$\frac{x+y}{2}$>y>$\sqrt{xy}$ | C. | x>y>$\frac{x+y}{2}$>$\sqrt{xy}$ | D. | x>$\frac{x+y}{2}$>$\sqrt{xy}$>y |
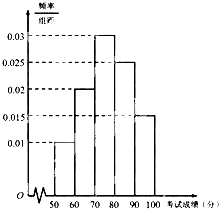 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].