题目内容
13．若$\sqrt{3}$位于$\frac{x+5}{x}$和$\frac{x+6}{x}$之间，求自然数x的取值．分析 由题意可得：$\frac{x+5}{x}$$＜\sqrt{3}＜$$\frac{x+6}{x}$，化为$\frac{5（\sqrt{3}+1）}{2}$＜x$＜3（\sqrt{3}+1）$，即可得出．
解答 解：由题意可得：$\frac{x+5}{x}$$＜\sqrt{3}＜$$\frac{x+6}{x}$，
化为$\frac{5}{\sqrt{3}-1}＜x＜\frac{6}{\sqrt{3}-1}$，
即$\frac{5（\sqrt{3}+1）}{2}$＜x$＜3（\sqrt{3}+1）$，
∴自然数x=8，7．
点评 本题考查了不等式的性质及其解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
相关题目
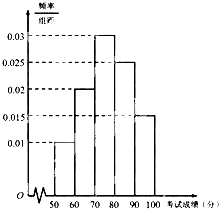某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．