题目内容
10.△ABC中,角A、B、C所对的边分别为a、b、c,且a=3,b=5,c=6,则$\overrightarrow{AB}$•$\overrightarrow{BC}$+$\overrightarrow{BC}$•$\overrightarrow{CA}$+$\overrightarrow{CA}$•$\overrightarrow{AB}$的值为( )| A. | -35 | B. | 35 | C. | -40 | D. | 40 |
分析 利用数量积的定义、余弦定理即可得出.
解答 解:由数量积的定义可得:$\overrightarrow{AB}$•$\overrightarrow{BC}$+$\overrightarrow{BC}$•$\overrightarrow{CA}$+$\overrightarrow{CA}$•$\overrightarrow{AB}$=-accosB-abcosC-bccosA
=-($\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}$+$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}$+$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2}$)
=-$\frac{{a}^{2}+{b}^{2}+{c}^{2}}{2}$
=-$\frac{{3}^{2}+{5}^{2}+{6}^{2}}{2}$
=-35.
故选:A.
点评 本题考查了数量积的定义、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
20.函数f(x)=$\frac{\sqrt{4-{x}^{2}}}{4-|x-4|}$是( )
| A. | 奇函数但不是偶函数 | B. | 偶函数但不是奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
5.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点(x,y)落在直线y=-x+5上的概率为( )
| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{4}$ |
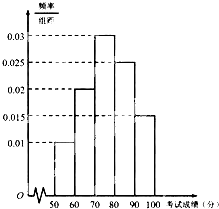 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].