题目内容
15.已知抛物线C的顶点在原点,对称轴是x轴,抛物线过点M($\frac{1}{2}$,1).(1)求C的方程;
(2)过C的焦点F作直线交抛物线于A,B两点,若|AB|=$\frac{25}{12}$,|AF|<|BF|,求|AF|.
分析 (1)通过设抛物线C的标准方程为y2=2px,代入点M($\frac{1}{2}$,1)计算可知p=1,进而可得结论;
(2)通过(1)可知焦点F($\frac{1}{2}$,0),设A(x1,y1)、B(x2,y2),设直线AB的方程为x=my+$\frac{1}{2}$,通过联立直线AB与抛物线方程,利用韦达定理及两点间距离公式计算可知m=±$\frac{\sqrt{6}}{12}$,进而利用抛物线的定义计算即得结论.
解答 解:(1)由题意可设抛物线C的标准方程为:y2=2px,
∵抛物线过点M($\frac{1}{2}$,1),
∴p=1,
所以抛物线C的方程为:y2=2x;
(2)由(1)可知焦点F($\frac{1}{2}$,0),设A(x1,y1)、B(x2,y2),
设直线AB的方程为:x=my+$\frac{1}{2}$,则
联立直线AB与抛物线方程,整理可知:y2-2my-1=0,
∴y1+y2=2m,y1y2=-1,△=4m2+4>0,
∴|AB|=$\sqrt{1+{m}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{1+{m}^{2}}$•$\sqrt{4{m}^{2}+4}$
=2(1+m2)
=$\frac{25}{12}$,
解得:m=±$\frac{\sqrt{6}}{12}$,
∴x1+x2=m(y1+y2)+1=$\frac{13}{12}$,
x1x2=m2y1y2+$\frac{m}{2}$(y1+y2)+$\frac{1}{4}$=$\frac{1}{4}$,
∴x1=$\frac{3}{4}$或x1=$\frac{1}{3}$,
∵|AF|<|BF|,
∴B($\frac{3}{4}$,y1)、A($\frac{1}{3}$,y2),
又∵抛物线C的准线方程为:x=-$\frac{1}{2}$,
∴|AF|=$\frac{1}{3}$+$\frac{1}{2}$=$\frac{5}{6}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案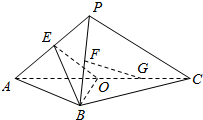 如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明).
如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明).