题目内容
【题目】
的内切圆与三边
的切点分别为
,已知
，内切圆圆心
,设点A的轨迹为R.
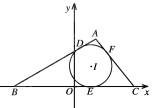
（1）求R的方程；
（2）过点C的动直线m交曲线R于不同的两点M,N，问在x轴上是否存在一定点Q（Q不与C重合），使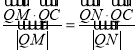
恒成立，若求出Q点的坐标，若不存在，说明理由.
【答案】(1)
；(2)存在
【解析】
试题(1)根据切线长定理可得，AB-AC=2.根据双曲线的定义可得点A的轨迹是双曲线的一支，即可得到轨迹方程.
(2)因为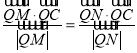
恒成立，通过化简可得等价结论，QC为∠MQN的角平分线.由直线MN垂直于x轴，显然存在点Q.当MN不垂直x轴时，依题意所求的结论等价转化于
，通过联立方程，利用韦达定理，即可求得点Q的横坐标.
试题解析：（1）设点
，由题知|AB|-|AC|=|BE|-|CE|=|CE|+2|OE|-|CE|=2
根据双曲线定义知，点A的轨迹是以B、C为焦点，实轴长为2的双曲线的右支除去点E（1，0），故R的方程为
（2）设点
由（I）可知
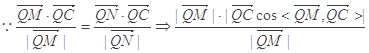
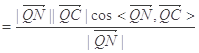
①当直线
轴时
点
在
轴上任何一点处都能使得
成立
②当直线MN不与轴垂直时，设直线
由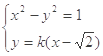
得
要使，只需
成立即
即
即
故
,故所求的点Q的坐标为时
使
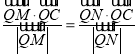成立.
【题目】若A1，A2，…，Am为集合A＝{1，2，…，n}（n≥2且n∈N*）的子集，且满足两个条件：
①A1∪A2∪…∪Am＝A；
②对任意的{x，y}A，至少存在一个i∈{1，2，3，…，m}，使Ai∩{x，y}＝{x}或{y}．则称集合组A1，A2，…，Am具有性质P．
如图，作n行m列数表，定义数表中的第k行第l列的数为akl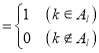
．
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
（1）当n＝4时，判断下列两个集合组是否具有性质P，如果是请画出所对应的表格，如果不是请说明理由；
集合组1：A1＝{1，3}，A2＝{2，3}，A3＝{4}；
集合组2：A1＝{2，3，4}，A2＝{2，3}，A3＝{1，4}．
（2）当n＝7时，若集合组A1，A2，A3具有性质P，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合A1，A2，A3；
（3）当n＝100时，集合组A1，A2，…，At是具有性质P且所含集合个数最小的集合组，求t的值及|A1|+|A2|+…|At|的最小值．（其中|Ai|表示集合Ai所含元素的个数）
