题目内容
【题目】若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl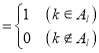 .
.
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
(1)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(2)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(3)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
【答案】(1)集合组1具有性质P,集合组2不具有性质P,理由见解析;(2)图见解析,A1={3,4,5,7},A2={2,4,6,7},A3={1,5,6,7};(3)304
【解析】
(1)根据题意检验两个集合组是否满足性质即可;
(2)一共7行对应1,2,3,4,5,6,7,七个数,其中每列的1或0代表这个集合里面有或者无对应的数,要求每行必须有1,任意两个数至少有一列只出现一个;
(3)条件①可知数表M中任意一行不全为0,由条件②可得数表M中任意两行不完全相同,结合排列组合知识求解.
(1)集合组1具有性质P.
所对应的数表为:
1 | 0 | 0 |
0 | 1 | 0 |
1 | 1 | 0 |
0 | 0 | 1 |
集合组2不具有性质P.
因为存在{2,3}{1,2,3,4},有{2,3}∩A1={2,3},{2,3}∩A2={2,3},{2,3}∩A3=,
与对任意的{x,y}A,都至少存在一个i∈{1,2,3},有Ai∩{x,y}={x}或{y}矛盾,
所以集合组A1={2,3,4},A2={2,3},A3={1,4}不具有性质P.…
(2)
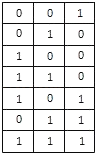
A1={3,4,5,7},A2={2,4,6,7},A3={1,5,6,7}.
(注:表格中的7行可以交换得到不同的表格,它们所对应的集合组也不同)
(3)设A1,A2,…,At所对应的数表为数表M,
因为集合组A1,A2,…,At为具有性质P的集合组,所以集合组A1,A2,…,At满足条件①和②,
由条件①:A1∪A2∪…∪At=A,可得对任意x∈A,都存在i∈{1,2,3,…,t}有x∈Ai,
所以axi=1,即第x行不全为0,所以由条件①可知数表M中任意一行不全为0.
由条件②知,对任意的{x,y}A,都至少存在一个i∈{1,2,3,…,t},使Ai∩{x,y}={x}或{y},所以axi,ayi一定是一个1一个0,即第x行与第y行的第i列的两个数一定不同.
所以由条件②可得数表M中任意两行不完全相同.
因为由0,1所构成的t元有序数组共有2t个,去掉全是0的t元有序数组,共有2t﹣1个,又因数表M中任意两行都不完全相同,所以100≤2t﹣1,所以t≥7.
又t=7时,由0,1所构成的7元有序数组共有128个,去掉全是0的数组,共127个,选择其中的100个数组构造100行7列数表,则数表对应的集合组满足条件①②,即具有性质P.所以t=7.
因为|A1|+|A2|+…+|At|等于表格中数字1的个数,
所以,要使|A1|+|A2|+…+|At|取得最小值,只需使表中1的个数尽可能少,
而t=7时,在数表M中,1的个数为1的行最多7行;1的个数为2的行最多C72=21行;1的个数为3的行最多C73=35行;1的个数为4的行最多C74=35行;
因为上述共有98行,所以还有2行各有5个1,
所以此时表格中最少有7+2×21+3×35+4×35+5×2=304个1.所以|A1|+|A2|+…+|At|的最小值为304.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
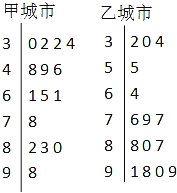
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.