题目内容
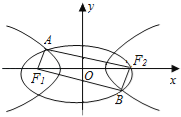
【题目】如图F1、F2是椭圆C1：
+y2=1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】试题分析:不妨设|AF1|=x，|AF2|=y，依题意
，解此方程组可求得x，y的值，利用双曲线的定义及性质即可求得C2的离心率．
解：设|AF1|=x，|AF2|=y，∵点A为椭圆C1：
+y2=1上的点，
∴2a=4，b=1，c=
；
∴|AF1|+|AF2|=2a=4，即x+y=4；①
又四边形AF1BF2为矩形，
∴
+
=
，即x2+y2=（2c）2=
=12，②
由①②得：
，解得x=2﹣
，y=2+，设双曲线C2的实轴长为2m，焦距为2n，
则2m=|AF2|﹣|AF1|=y﹣x=2，2n=2c=2
，
∴双曲线C2的离心率e=
=
=
．
故选D．
练习册系列答案
相关题目
【题目】某商场经销某商品，根据以往资料统计，顾客采用的付款期数
的分布列为：
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销该商品，可采用不同形式的分期付款，付款的期数
（单位： 
）与商场经销一件商品的利润
（单位：元）满足如下关系： 
（Ⅰ）若记事件“购买该商品的3位顾客中，至少有1位采用一次性全额付款方式”为
，试求事件
的概率
；
（Ⅱ）求商场经销一件商品的利润
的分布列及期望
．
