ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΒΊ«χ2009Ρξ÷Ν2015Ρξ≈©¥εΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κyΘ®ΒΞΈΜΘΚ«ß‘ΣΘ©ΒΡ ΐΨί»γ±μΘΚ
ΡξΖί | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
ΡξΖί¥ζΚ≈t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
»ΥΨυ¥Ω ’»κy | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
Θ®1Θ©«σyΙΊ”ΎtΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
Θ®2Θ©άϊ”ΟΘ®1Θ©÷–ΒΡΜΊΙιΖΫ≥ΧΘ§Ζ÷Έω2009Ρξ÷Ν2015ΡξΗΟΒΊ«χ≈©¥εΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κΒΡ±δΜ·«ιΩωΘ§≤Δ‘Λ≤βΗΟΒΊ«χ2017Ρξ≈©¥εΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κΘ°
ΗΫΘΚΜΊΙι÷±œΏΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ 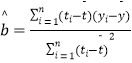 Θ°
Θ° ![]() Θ°
Θ°
≤ΈΩΦ ΐΨίΘΚΘ®©¹3Θ©ΓΝΘ®©¹1.4Θ©+Θ®©¹2Θ©ΓΝΘ®©¹1Θ©+Θ®©¹1Θ©ΓΝΘ®©¹0.7Θ©+1ΓΝ0.5+2ΓΝ0.9+3ΓΝ1.6=14Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ”…ΥυΗχ ΐΨίΦΤΥψΒΟ
![]() =
= ![]() =4Θ§
=4Θ§
![]() =
= ![]() =4.4Θ§
=4.4Θ§
Θ®ti©¹ ![]() Θ©2=9+4+1+0+1+4+9=28Θ§
Θ©2=9+4+1+0+1+4+9=28Θ§
![]() Θ®ti©¹
Θ®ti©¹ ![]() Θ©Θ®yi©¹
Θ©Θ®yi©¹ ![]() Θ©=Θ®©¹3Θ©ΓΝΘ®©¹1.4Θ©+Θ®©¹2Θ©ΓΝΘ®©¹1Θ©+Θ®©¹1Θ©ΓΝΘ®©¹0.7Θ©+1ΓΝ0.5+2ΓΝ0.9+3ΓΝ1.6=14Θ°Θ§
Θ©=Θ®©¹3Θ©ΓΝΘ®©¹1.4Θ©+Θ®©¹2Θ©ΓΝΘ®©¹1Θ©+Θ®©¹1Θ©ΓΝΘ®©¹0.7Θ©+1ΓΝ0.5+2ΓΝ0.9+3ΓΝ1.6=14Θ°Θ§
 =
= ![]() =0.5Θ§
=0.5Θ§ ![]() =4.3©¹0.5ΓΝ4=2.3Θ§
=4.3©¹0.5ΓΝ4=2.3Θ§
Υυ«σΜΊΙιΖΫ≥ΧΈΣy=0.5t+2.3
Θ®2Θ©ΫβΘΚ”…Θ®1Θ©÷ΣΘ§b=0.5ΘΨ0Θ§Ι 2009Ρξ÷Ν2015ΡξΗΟΒΊ«χΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κ÷πΡξ‘ωΦ”Θ§ΤΫΨυΟΩΡξ‘ωΦ”0.5«ß‘ΣΘ°
ΫΪ2017ΡξΒΡΡξΖί¥ζΚ≈t=9¥ζ»κΘ®1Θ©ΒΡΜΊΙιΖΫ≥ΧΘ§ΒΟy=6.8Θ§
Ι ‘Λ≤βΗΟΒΊ«χ2017ΡξΗΟΒΊ«χΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κ‘ΦΈΣ6.8«ß‘ΣΘ°
ΓΨΫβΈωΓΩΘ®1Θ©œ»«σ≥ωΡξΖί¥ζΚ≈tΚΆ»ΥΨυ¥Ω ’»κyΒΡΤΫΨυ ΐΘ§ΒΟΒΫ’βΉι ΐΨίΒΡ―υ±Ψ÷––ΡΒψΘ§άϊ”ΟΉν–ΓΕΰ≥ΥΖ®«σ≥ωœΏ–‘ΜΊΙιΖΫ≥ΧΒΡœΒ ΐΘ§¥ζ»κ―υ±Ψ÷––ΡΒψ«σ≥ωaΒΡ÷ΒΘ§–¥≥ωœΏ–‘ΜΊΙιΖΫ≥ΧΘΜΘ®2Θ©”…Θ®1Θ©÷ΣΘ§b=0.5ΘΨ0Θ§2009Ρξ÷Ν2015ΡξΗΟΒΊ«χΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κ÷πΡξ‘ωΦ”Θ§ΤΫΨυΟΩΡξ‘ωΦ”0.5«ß‘ΣΘ§«σΒΟ2017ΡξΒΡΡξΖί¥ζΚ≈t=9¥ζ»κΘ®1Θ©ΒΡΜΊΙιΖΫ≥ΧΘ§ΒΟyΒΡ÷ΒΘ°

ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΨ≠œζΡ≥…ΧΤΖΘ§ΗυΨί“‘ΆυΉ ΝœΆ≥ΦΤΘ§ΙΥΩΆ≤…”ΟΒΡΗΕΩνΤΎ ΐ![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
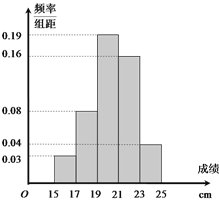
…Χ≥ΓΨ≠œζΗΟ…ΧΤΖΘ§Ω…≤…”Ο≤ΜΆ§–Έ ΫΒΡΖ÷ΤΎΗΕΩνΘ§ΗΕΩνΒΡΤΎ ΐ![]() Θ®ΒΞΈΜΘΚ
Θ®ΒΞΈΜΘΚ ![]() Θ©”κ…Χ≥ΓΨ≠œζ“ΜΦΰ…ΧΤΖΒΡάϊ»σ
Θ©”κ…Χ≥ΓΨ≠œζ“ΜΦΰ…ΧΤΖΒΡάϊ»σ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©¬ζΉψ»γœ¬ΙΊœΒΘΚ
Θ®ΒΞΈΜΘΚ‘ΣΘ©¬ζΉψ»γœ¬ΙΊœΒΘΚ 
Θ®ΔώΘ©»τΦ« ¬ΦΰΓΑΙΚ¬ρΗΟ…ΧΤΖΒΡ3ΈΜΙΥΩΆ÷–Θ§÷Ν…Ό”–1ΈΜ≤…”Ο“Μ¥Έ–‘»ΪΕνΗΕΩνΖΫ ΫΓ±ΈΣ![]() Θ§ ‘«σ ¬Φΰ
Θ§ ‘«σ ¬Φΰ![]() ΒΡΗ≈¬
ΒΡΗ≈¬ ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©«σ…Χ≥ΓΨ≠œζ“ΜΦΰ…ΧΤΖΒΡάϊ»σ![]() ΒΡΖ÷≤ΦΝ–ΦΑΤΎΆϊ
ΒΡΖ÷≤ΦΝ–ΦΑΤΎΆϊ![]() Θ°
Θ°