Question

【题目】在三棱锥P－ABC中，D为AB的中点。

（1）与BC平行的平面PDE交AC于点E，判断点E在AC上的位置并说明理由如下：

（2）若PA＝PB，且△PCD为锐角三角形，又平面PCD⊥平面ABC，求证：AB⊥PC。

Answer 1

【答案】（1）为中点（2）详见解析

【解析】

试题分析：（1）实质为由线面平行转化为线线平行，即由平面得，因为为的中点，所以为中点；（2）先找出平几中垂直条件：因为，为的中点，所以，再根据面面垂直转化为线面垂直：作于，则由平面平面得平面，从而，因而平面，即证．

试题解析：

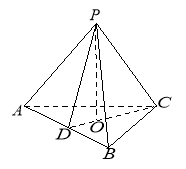
（1）解：为中点．理由如下：

平面交于，即平面平面，

而平面，平面，所以， 4分

在中，因为为的中点，所以为中点； 7分

（2）证：因为，为的中点，所以，

因为平面平面，平面平面，

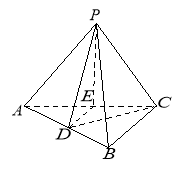
在锐角所在平面内作于，则平面，…10分

因为平面，所以

又，平面，则平面，

又平面，所以． 14分