题目内容
设F1、F2是双曲线 的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
| A.1 | B. | C.2 | D. |
A
解析试题分析:在△F PF
PF 中, | F
中, | F F
F |
| =" |" PF
=" |" PF |
| +| PF
+| PF |
| =20,∵| | PF
=20,∵| | PF |-| PF
|-| PF | |=4,∴-2| PF
| |=4,∴-2| PF |·| PF
|·| PF |="(|" PF
|="(|" PF |-| PF
|-| PF |)
|) -| PF
-| PF |
| +| PF
+| PF |
| =-4,∴| PF
=-4,∴| PF |·| PF
|·| PF |=2,∴
|=2,∴ =
= | PF
| PF |·| PF
|·| PF |=1,故选A
|=1,故选A
考点:本题考查了双曲线的性质
点评:解决双曲线中的焦点三角形问题的关键是“| PF |·| PF
|·| PF |”形式的配凑,将双曲线的定义及图形的平面几何属性“和谐”地结合起来,从而达到简化运算过程,提示问题的本质特征
|”形式的配凑,将双曲线的定义及图形的平面几何属性“和谐”地结合起来,从而达到简化运算过程,提示问题的本质特征

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线 与直线
与直线 交于A,B两点,其中A点的坐标是
交于A,B两点,其中A点的坐标是 .该抛物线的焦点为F,则
.该抛物线的焦点为F,则 ( )
( )
| A.7 | B. | C.6 | D.5 |
已知
 的顶点
的顶点 、
、 分别为双曲线
分别为双曲线 的左右焦点,顶点
的左右焦点,顶点 在双曲线
在双曲线 上,则
上,则 的值等于
的值等于
A. | B. | C. | D. |
 的焦点相同,则双曲线C的标准方程是( )
的焦点相同,则双曲线C的标准方程是( )



 、
、 与双曲线
与双曲线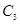 、
、 的离心率分别是
的离心率分别是 、
、 与
与 、
、 , 则
, 则




 的右焦点作倾斜角为
的右焦点作倾斜角为 的直线
的直线 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则 ( )
( ) C . -3或
C . -3或




 (a>0,b>0)的左、右焦点,过F1的直线
(a>0,b>0)的左、右焦点,过F1的直线 与
与 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为



 的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q 两点,当四边形PF1QF2面积最大时,
的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q 两点,当四边形PF1QF2面积最大时, 的值等于( )
的值等于( )