题目内容
已知F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是( )
A. | B. | C. | D. |
A
解析试题分析:因为F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,且△ABF2是正三角形,所以由椭圆的对称性可知,AB垂直于x轴,将x=c代入椭圆方程,可得|AB|=2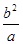 ,从而在直角三角形中
,从而在直角三角形中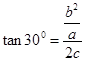 ,即
,即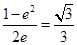 ,解得e=
,解得e= ,故选A。
,故选A。
考点:本题主要考查椭圆的定义,椭圆的几何性质。
点评:简单题,涉及椭圆的焦点三角形问题,往往要利用椭圆的定义。本题同时关注三角形的特征。

练习册系列答案
相关题目
已知抛物线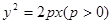 与双曲线
与双曲线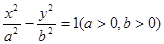 有相同的焦点
有相同的焦点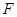 ,点
,点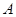 是两曲线的交点,且
是两曲线的交点,且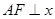 轴,则双曲线的离心率为( )
轴,则双曲线的离心率为( )
A.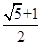 | B.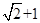 | C.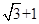 | D.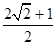 |
下列双曲线中,渐近线方程是 的是
的是
A. | B. | C. | D. |
设F1、F2是双曲线 的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
| A.1 | B. | C.2 | D. |
双曲线 的实轴长是虚轴长的2倍,则rn=
的实轴长是虚轴长的2倍,则rn=
A. | B. | C.2 | D.4 |
焦点为(0,6)且与双曲线 有相同的渐近线的双曲线方程是( )
有相同的渐近线的双曲线方程是( )
A. | B. | C. | D. |
设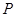 是椭圆
是椭圆 上的点,
上的点,  、
、 是椭圆的两个焦点,则
是椭圆的两个焦点,则 的值为
的值为
| A. 10 | B. 8 | C.6 | D.4 |
 是非零实数,则方程
是非零实数,则方程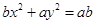 及
及 所表示的图形可能是( )
所表示的图形可能是( )
 ,过左焦点F1作斜率为
,过左焦点F1作斜率为 的直线交双曲线的右支于点P,且
的直线交双曲线的右支于点P,且 轴平分线段F1P,则双曲线的离心率是( )
轴平分线段F1P,则双曲线的离心率是( )


