题目内容
【题目】已知函数![]() 有两个不同零点
有两个不同零点![]() 、
、![]() (
(![]() ),设函数
),设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值记为
的最大值记为![]() ,最小值记为
,最小值记为![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)当![]() 时,试问以
时,试问以![]() 、
、![]() 、
、![]() 为长度的线段能否组成一个三角形,如果不一定,进一步求出
为长度的线段能否组成一个三角形,如果不一定,进一步求出![]() 的取值范围,使它们能组成一个三角形;
的取值范围,使它们能组成一个三角形;
(3)求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)应用韦达定理计算;
(2)用求根公式求出![]() ,得出
,得出![]() ,只要
,只要![]() ,以
,以![]() 、
、![]() 、
、![]() 为长度的线段就能构成三角形;
为长度的线段就能构成三角形;
(3)求出导函数![]() ,由已知可得
,由已知可得![]() 时,
时,![]() ,从而
,从而![]() ,即
,即![]() 递增,这样就可求出
递增,这样就可求出![]() 和
和![]() ,代入计算
,代入计算![]() ,注意韦达定理的代入.
,注意韦达定理的代入.
(1)由题意![]() 恒成立,∴
恒成立,∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)![]() ,方程
,方程![]() 的两根为
的两根为![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,
易知![]() ,而
,而![]() ,
,
若以![]() 、
、![]() 、
、![]() 为长度的线段能组成一个三角形,则
为长度的线段能组成一个三角形,则![]() ,
,
即![]() ,
,![]() ,
,
∴![]() .
.
∴当![]() 时,以
时,以![]() 、
、![]() 、
、![]() 为长度的线段能组成一个三角形.
为长度的线段能组成一个三角形.
(3)![]() ,
,
∵![]() 是方程
是方程![]() 的两个根,
的两个根,
∴![]() ,
,![]()
当![]() 时,
时,![]() ,从而
,从而![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
∴![]()
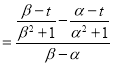
![]()
![]()
![]()
![]() .
.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目