题目内容
【题目】已知函数![]() 在区间
在区间![]() 上的最大值为9,最小值为1,记
上的最大值为9,最小值为1,记![]()
(1)求实数![]() ,
,![]() 的值;
的值;
(2)若不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,
,![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,如果存在一个常数
个小区间,如果存在一个常数![]() ,使得和式
,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数.试判断函数
上的有界变差函数.试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由(
的最小值;若不是,请说明理由(![]() 表示
表示![]() )
)
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)是,最小值为10
;(3)是,最小值为10
【解析】
(1)由已知![]() ,根据二次函数对称轴公式:
,根据二次函数对称轴公式:![]() ,得
,得![]() 的对称轴为:
的对称轴为:![]() ,结合函数的单调性及最值,即可得到关于
,结合函数的单调性及最值,即可得到关于![]() ,
,![]() 的方程组,进而解得
的方程组,进而解得![]() ,
,![]() 的值;
的值;
(2)由(1)得参数![]() ,
,![]() 的值,代入
的值,代入![]() 可得函数解析式,根据二次函数的图像和性质,可将问题转化为距离
可得函数解析式,根据二次函数的图像和性质,可将问题转化为距离![]() 轴距离远近的问题,得到关于
轴距离远近的问题,得到关于![]() 的方程,即可求得
的方程,即可求得![]() 的取值范围;
的取值范围;
(3)根据有界变差函数的定义,我们先将区间![]() 进行划分,分成
进行划分,分成![]() ,
,![]() 两个区间进行分别判断,进而判断
两个区间进行分别判断,进而判断![]() 是否恒成立,从而得出结论.
是否恒成立,从而得出结论.
(1)![]()
![]()
![]() ,是开口向上的二次函数
,是开口向上的二次函数
根据二次函数对称轴公式:![]() ,得
,得![]() 的对称轴为:
的对称轴为:![]()
由二次函数图像可知![]() 在
在![]() 上是单调递增故:
上是单调递增故:![]() ,
,![]()
得:![]() 解得:
解得:![]()
(2)![]()
![]()
又![]()
![]() 故
故![]() 为偶函数
为偶函数
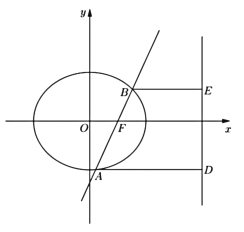
画出![]() 图像:
图像:
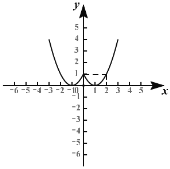
由图像可知要保证:![]() 即:
即:![]()
则:![]() 或
或![]() 解得:
解得:![]() 或
或![]()
所以实数![]() 的取值范围为:
的取值范围为:![]() .
.
(3)![]() 函数
函数![]() 为
为![]() 上的有界变差函数
上的有界变差函数
又![]() 函数
函数![]() 为
为![]() 上的单调递减函数,在
上的单调递减函数,在![]() 上是单调递增函数
上是单调递增函数
且对任意划分![]() :
:![]()
有![]()
![]()
![]()
![]() 恒成立.
恒成立.
且对任意划分![]() :
:![]()
有![]()
![]()
![]()
![]()
![]() 可得
可得![]()
综上所述:存在常数![]() ,使得
,使得![]() 恒成立,
恒成立,![]() 的最小值为
的最小值为![]() .
.

 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 30 | 18 | 48 |
大于40岁 | 20 | 32 | 52 |
总计 | 50 | 50 | 100 |
(1)用分层抽样方法在收看文艺节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为大于40岁的概率.