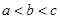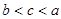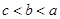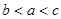题目内容
(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对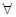 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe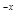 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对
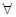 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe
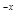 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.(1)[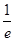 ,e](2)①分别求f(x)和g(x)在点(x1, f (x1))和(x2, g(x2))的切线,记为公切线,所以斜率和截距分别相同,从而得证结论;②(-∞,1]
,e](2)①分别求f(x)和g(x)在点(x1, f (x1))和(x2, g(x2))的切线,记为公切线,所以斜率和截距分别相同,从而得证结论;②(-∞,1]
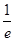 ,e](2)①分别求f(x)和g(x)在点(x1, f (x1))和(x2, g(x2))的切线,记为公切线,所以斜率和截距分别相同,从而得证结论;②(-∞,1]
,e](2)①分别求f(x)和g(x)在点(x1, f (x1))和(x2, g(x2))的切线,记为公切线,所以斜率和截距分别相同,从而得证结论;②(-∞,1]试题分析:(1)依题意对
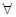 x∈(0,+∞)均有ex≥kx≥lnx成立,
x∈(0,+∞)均有ex≥kx≥lnx成立,即对任意
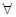 x∈(0,+∞)均有
x∈(0,+∞)均有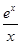 ≥k≥
≥k≥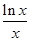 成立, ……1分
成立, ……1分∴(
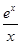 )min≥k≥
)min≥k≥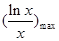 ,
,因为
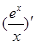 =
=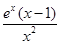 ,故
,故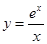 在(0,1)上减,(1,+∞)增,
在(0,1)上减,(1,+∞)增,∴(
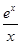 )min=e,
)min=e,又
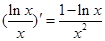 ,故
,故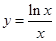 在(0,e)上减,(e,+∞)增,
在(0,e)上减,(e,+∞)增,∴
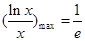 ,即k的取值范围是[
,即k的取值范围是[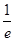 ,e] . ……5分
,e] . ……5分(2)由题知:h(x)即为y-e
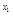 = e
= e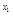 (x-x1)即y=e
(x-x1)即y=e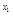 ·x+ e
·x+ e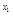 -x1 e
-x1 e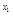 ,
,也为y=lnx2=
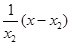 即y=
即y=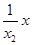 +lnx2-1,
+lnx2-1,∴
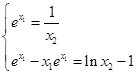 , ……6分
, ……6分又x1=0 ∴e
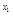 >1 即
>1 即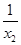 >1
>1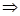 x1>1即x1>1>x2, ……8分
x1>1即x1>1>x2, ……8分(3)令F(x)=ax2-x+xe
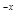 +1(x≥x1),
+1(x≥x1),∴F′(x)= -1-xe
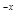 +e
+e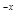 =-1+e
=-1+e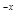 (1-x)( x≥x1)
(1-x)( x≥x1)又x≥x1>1 F′(x)= -1-xe
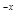 +e
+e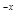 =-1+e
=-1+e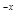 (1-x)<0,
(1-x)<0,即F(x)=ax2-x+xe
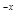 +1(x≥x1)单减,
+1(x≥x1)单减,所以只要F(x)≤F(x1)= ax2-x1+1xe
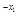 +1≤0,
+1≤0,即a+ x1-x1e
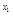 + e
+ e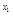 ≤0. ……12分
≤0. ……12分由
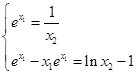 ,
,∴
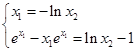 ,
,即
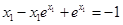
故只要
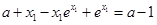 ≤0得:a≤1,
≤0得:a≤1,综上,实数a的取值范围是(-∞,1]. ……14分
点评:导数是研究函数性质的有力工具,要熟练应用,而恒成立问题一般要转化为最值问题解决.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
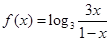 .
. 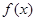 的图像关于点
的图像关于点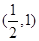 对称;
对称;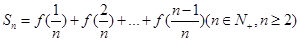 ,求
,求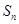 ;
;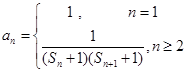
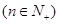 ,
,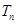 为数列
为数列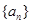 的前
的前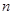 项和,若
项和,若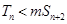 对一切
对一切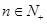 都成立,试求实数
都成立,试求实数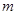 的取值范围.
的取值范围.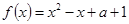
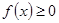 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。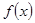 在区间
在区间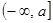 上的最小值
上的最小值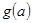 的表达式。
的表达式。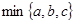 为
为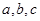 中的最小值,设
中的最小值,设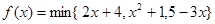 ,则
,则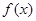 的最大值是 .
的最大值是 .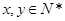 ,且
,且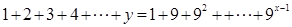 ,当
,当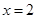 时,
时, 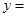 ;若把
;若把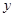 表示成
表示成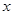 的函数,其解析式是
的函数,其解析式是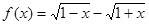 。
。 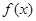 的定义域;
的定义域;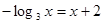 的根所在的区间为 ( )
的根所在的区间为 ( ) 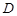 是函数
是函数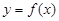 定义域内的一个区间,若存在
定义域内的一个区间,若存在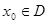 ,使
,使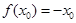 ,
,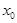 是
是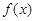 的一个“次不动点”,也称
的一个“次不动点”,也称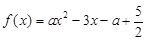 在区间
在区间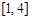 上存在次不动点,则实数
上存在次不动点,则实数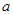 的取值范围
的取值范围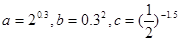 ,则
,则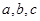 的大小关系是( )
的大小关系是( )