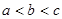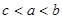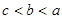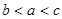题目内容
已知函数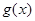 是
是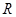 上的奇函数,且当
上的奇函数,且当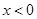 时
时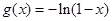 ,函数
,函数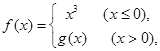 若
若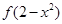 >
>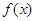 ,则实数
,则实数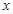 的取值范围是
的取值范围是
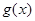 是
是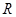 上的奇函数,且当
上的奇函数,且当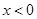 时
时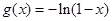 ,函数
,函数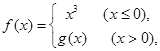 若
若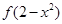 >
>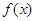 ,则实数
,则实数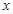 的取值范围是
的取值范围是A.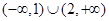 | B.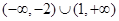 |
| C.(1,2) | D. |
D
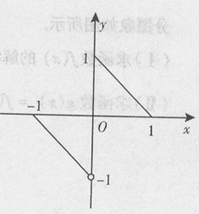
试题分析:∵奇函数g(x)满足当x<0时,g(x)=-ln(1-x),
∴当x>0时,g(-x)=-ln(1+x)=-g(x),
得当x>0时,g(x)=-g(-x)=ln(1+x)
∴f(x)的表达式为
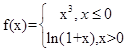 ,
,∵
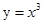 在(-∞,0)上是增函数,y=ln(1+x)在(0,+∞)上是增函数,
在(-∞,0)上是增函数,y=ln(1+x)在(0,+∞)上是增函数,∴f(x)在其定义域上是增函数,
由此可得:
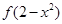 >
>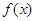 等价于
等价于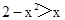 ,解之得-2<x<1,
,解之得-2<x<1,故选D。
点评:中档题,涉及抽象函数不等式问题,一般的要通过研究函数的单调性,转化成具体不等式求解。本题定义
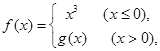 人为地增大了难度,易于出错。
人为地增大了难度,易于出错。
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 的最大允许值是多少?
的最大允许值是多少?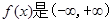 上的奇函数,且
上的奇函数,且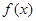 的图象关于直线x=1对称,当
的图象关于直线x=1对称,当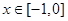 时,
时,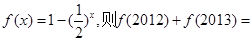 .
.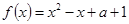
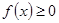 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。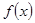 在区间
在区间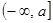 上的最小值
上的最小值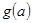 的表达式。
的表达式。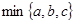 为
为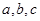 中的最小值,设
中的最小值,设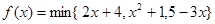 ,则
,则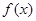 的最大值是 .
的最大值是 .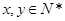 ,且
,且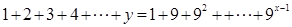 ,当
,当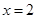 时,
时, 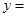 ;若把
;若把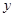 表示成
表示成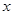 的函数,其解析式是
的函数,其解析式是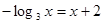 的根所在的区间为 ( )
的根所在的区间为 ( ) 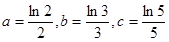 ,则【 】
,则【 】