题目内容
【题目】已知椭圆C: ![]() 的右焦点为F,右顶点为A,设离心率为e,且满足
的右焦点为F,右顶点为A,设离心率为e,且满足![]() ,其中O为坐标原点.
,其中O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点![]() 的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(1)根据![]() ,解得c值,即可得椭圆的方程;
,解得c值,即可得椭圆的方程;
(Ⅱ)联立l与椭圆C的方程,得![]() ,
,
得![]() ,
, ![]() .所以
.所以![]() ,又O到l的距离
,又O到l的距离![]() .所以△OMN的面积
.所以△OMN的面积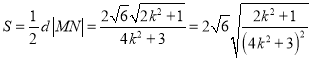 求最值即可.
求最值即可.
试题解析:(Ⅰ)设椭圆的焦半距为c,则|OF| = c,|OA| = a,|AF| = ![]() .
.
所以![]() ,其中
,其中![]() ,又
,又![]() ,联立解得
,联立解得![]() ,
, ![]() .
.
所以椭圆C的方程是![]() .
.
(Ⅱ)由题意直线不能与x轴垂直,否则将无法构成三角形.
当直线l与x轴不垂直时,设其斜率为k,那么l的方程为![]() .
.
联立l与椭圆C的方程,消去y,得![]() .
.
于是直线与椭圆有两个交点的充要条件是Δ=![]() ,这显然大于0.
,这显然大于0.
设点![]() ,
, ![]() .
.
由根与系数的关系得![]() ,
, ![]() .所以
.所以![]() ,又O到l的距离
,又O到l的距离![]() .
.
所以△OMN的面积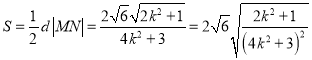 .
. ![]() ,那么
,那么![]() ,当且仅当t = 3时取等.
,当且仅当t = 3时取等.
所以△OMN面积的最大值是![]() .
.
点睛:本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
