题目内容
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() +3(﹣1≤x≤2).
+3(﹣1≤x≤2).
(1)若λ= ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)若函数f(x)的最小值是1,求实数λ的值.
【答案】
(1)解: ![]() (﹣1≤x≤2)
(﹣1≤x≤2)
设 ![]() ,得g(t)=t2﹣2λt+3(
,得g(t)=t2﹣2λt+3( ![]() ).
).
当 ![]() 时,
时, ![]() (
( ![]() ).
).
所以 ![]() ,
, ![]() .
.
所以 ![]() ,
, ![]() ,
,
故函数f(x)的值域为[ ![]() ,
, ![]() ]
]
(2)解:由(1)g(t)=t2﹣2λt+3=(t﹣λ)2+3﹣λ2( ![]() )
)
①当 ![]() 时,
时, ![]() ,
,
令 ![]() ,得
,得 ![]() ,不符合舍去;
,不符合舍去;
②当 ![]() 时,
时, ![]() ,
,
令﹣λ2+3=1,得 ![]() ,或
,或 ![]() ,不符合舍去;
,不符合舍去;
③当λ>2时,g(t)min=g(2)=﹣4λ+7,
令﹣4λ+7=1,得 ![]() ,不符合舍去.
,不符合舍去.
综上所述,实数λ的值为 ![]()
【解析】(1)化简 ![]() (﹣1≤x≤2),再利用换元法得g(t)=t2﹣2λt+3(
(﹣1≤x≤2),再利用换元法得g(t)=t2﹣2λt+3( ![]() );从而代入λ=
);从而代入λ= ![]() 求函数的值域;(2)g(t)=t2﹣2λt+3=(t﹣λ)2+3﹣λ2(
求函数的值域;(2)g(t)=t2﹣2λt+3=(t﹣λ)2+3﹣λ2( ![]() ),讨论λ以确定函数的最小值及最小值点,从而求λ.
),讨论λ以确定函数的最小值及最小值点,从而求λ.
【考点精析】本题主要考查了函数的值域和函数的最值及其几何意义的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.

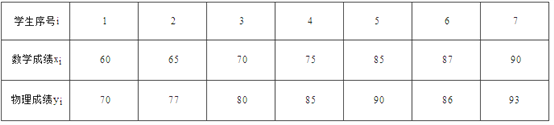
【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地有![]() ,
, ![]() 两种“共享单车”(以下简称
两种“共享单车”(以下简称![]() 型车,
型车, ![]() 型车).某学习小组7名同学调查了该地区共享单车的使用情况.
型车).某学习小组7名同学调查了该地区共享单车的使用情况.
(Ⅰ)某日该学习小组进行一次市场体验,其中4人租到![]() 型车,3人租到
型车,3人租到![]() 型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到
型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到![]() 型车的概率;
型车的概率;
(Ⅱ)根据已公布的2016年该地区全年市场调查报告,小组同学发现3月,4月的用户租车情况城现如表使用规律.例如,第3个月租![]() 型车的用户中,在第4个月有
型车的用户中,在第4个月有![]() 的用户仍租
的用户仍租![]() 型车.
型车.
第3个月 第4个月 | 租用 | 租用 |
租用 |
|
|
租用 |
|
|
若认为2017年该地区租用单车情况与2016年大致相同.已知2017年3月该地区租用![]() ,
,![]() 两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
【题目】(本小题满分12分)
微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有![]() ﹪的把握认为“微信控”与“性别”有关?
﹪的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 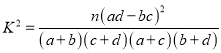 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |