题目内容
2. 如图,在五面体ABCDEF中,△EAD为正三角形,四边形ABCD为平行四边形,EF∥AB,∠DAB=60°,AB=2AD=4.
如图,在五面体ABCDEF中,△EAD为正三角形,四边形ABCD为平行四边形,EF∥AB,∠DAB=60°,AB=2AD=4.(1)若G是FC的中点,求证:AF∥平面GBD;
(2)若二面角E-AD-B为45°,$AF=\sqrt{6}$,求直线AF与平面ABCD所成的角.
分析 (1)连接AC交BD于O,连OG推出OG∥AF,利用直线与平面平行的判定定理证明AF∥平面GBD.
(2)取AD,AB的中点依次为M,N,连接MN,EM,DN,说明EMN是二面角E-AD-B的平面角,∠EMN=45°,然后说明∠FAQ为直线AF与平面ABCD所成的角,通过解三角形求解即可.
解答 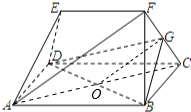 (1)证明:连接AC交BD于O,连OG,∵四边形ABCD为平行四边形∴O是AC中点
(1)证明:连接AC交BD于O,连OG,∵四边形ABCD为平行四边形∴O是AC中点
∵G是FC的中点∴OG是△CAF的中位线∴OG∥AF…(2分)
∵AF?平面GBD,OG?平面GBD…(4分)
∴AF∥平面GBD…(5分)
(2)解:取AD,AB的中点依次为M,N,连接MN,EM,DN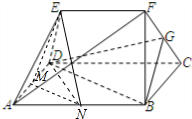
∵△EAD为正三角形∴EM⊥AD∵AD=2∴$EM=\sqrt{3}$,
∵∠DAB=60°,$AN=\frac{1}{2}AB=AD=2$,∴△NAD为正三角形∴NM⊥AD
∴∠EMN是二面角E-AD-B的平面角∴∠EMN=45°…(8分)
∵NM,EM是平面EMN内的两条相交直线∴AD⊥平面EMN…(9分)
∵AD?平面ABCD,∴平面EMN⊥平面ABCD…(10分)
作EP⊥MN,P为垂足,∵MN是平面EMN与平面ABCD的交线
∴EP⊥平面ABCD,∴在直角EMP中,$EP=\frac{{\sqrt{6}}}{2}$是点E到平面ABCD的距离 …(11分)
作FQ⊥平面ABCD,Q为垂足,∴∠FAQ为直线AF与平面ABCD所成的角
∵EF∥AB,AB?平面ABCD,EF?平面ABCD
∴EF∥平面ABCD,∴$FQ=EP=\frac{{\sqrt{6}}}{2}$
∴$sin∠FAQ=\frac{FQ}{AF}=\frac{1}{2}$,∴∠FAQ=30°…(13分)
点评 本题考查直线余平米平行的判定定理的应用,二面角以及直线与平面所成角的求法,考查计算能力以及空间想象能力.

| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 3 | B. | $\sqrt{3}$ | C. | 7 | D. | $\sqrt{7}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 若l∥α,l∥β,则α∥β | B. | 若l∥α,m?α,则l∥m | C. | 若α⊥β,l∥α,则l⊥β | D. | 若l⊥α,m?α,则l⊥m |
