题目内容
11.设P(x1,y1)是圆O1:x2+y2=9上的点,圆O2的圆心为Q(a,b),半径为1,则(a-x1)2+(b-y1)2=1是圆O1与圆O2相切的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由圆O2的圆心为Q(a,b),半径为1,可得圆O2的方程为:(x-a)2+(y-b)2=1.可得圆O1与圆O2相切的充要条件为:a2+b2=4或a2+b2=16.即可判断出.
解答 解:由圆O2的圆心为Q(a,b),半径为1,可得圆O2的方程为:(x-a)2+(y-b)2=1.
可得圆O1与圆O2相切的充要条件为:a2+b2=4或a2+b2=16.
∴(a-x1)2+(b-y1)2=1是圆O1与圆O2相切的既不充分也不必要条件.
故选:D.
点评 本题考查了不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
19.已知集合A={x|x2=a},B={-1,0,1},则a=1是A⊆B的( )
| A. | 充分不必要条件 | B. | 必要不充分条 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.在四面体S-ABC中,SA⊥平面ABC,∠BAC=120°,SA=AC=2,AB=1,则该四面体的外接球的表面积为( )
| A. | 11π | B. | 7π | C. | $\frac{10π}{3}$ | D. | $\frac{40π}{3}$ |
1.已知双曲线$\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{{a}^{2}}$=1过点(-1,2),则该双曲线的渐近线方程为( )
| A. | y=±$\frac{5\sqrt{2}}{2}$ | B. | y=±x | C. | y=±$\sqrt{2}$x | D. | y=±$\frac{\sqrt{2}}{2}$x |
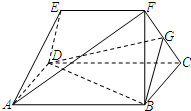 如图,在五面体ABCDEF中,△EAD为正三角形,四边形ABCD为平行四边形,EF∥AB,∠DAB=60°,AB=2AD=4.
如图,在五面体ABCDEF中,△EAD为正三角形,四边形ABCD为平行四边形,EF∥AB,∠DAB=60°,AB=2AD=4.