Question

【题目】设函数，为f（x）的导函数．

（1）若a=b=c，f（4）=8，求a的值；

（2）若a≠b，b=c，且f（x）和的零点均在集合中，求f（x）的极小值；

（3）若，且f（x）的极大值为M，求证:M≤．

Answer 1

【答案】（1）；

（2）见解析；

（3）见解析.

【解析】

（1）由题意得到关于a的方程，解方程即可确定a的值；

（2）由题意首先确定a,b,c的值从而确定函数的解析式，然后求解其导函数，由导函数即可确定函数的极小值.

（3）由题意首先确定函数的极大值M的表达式，然后可用如下方法证明题中的不等式：

解法一：由函数的解析式结合不等式的性质进行放缩即可证得题中的不等式；

解法二：由题意构造函数，求得函数在定义域内的最大值，

因为，所以．

当时，．

令，则．

令，得．列表如下：

	+	0	–
		极大值

所以当时，取得极大值，且是最大值，故．

所以当时，，因此．

（1）因为，所以．

因为，所以，解得．

（2）因为，

所以，

从而．令，得或．

因为，都在集合中，且，

所以．

此时，．

令，得或．列表如下：

				1
	+	0	–	0	+
		极大值		极小值

所以的极小值为．

（3）因为，所以，

．

因为，所以，

则有2个不同的零点，设为．

由，得．

列表如下：

	+	0	–	0	+
		极大值		极小值

所以的极大值．

解法一：

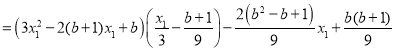
．因此．

解法二：

因为，所以．

当时，．

令，则．

令，得．列表如下：

	+	0	–
		极大值

所以当时，取得极大值，且是最大值，故．

所以当时，，因此．