题目内容
8．关于x的方程x2-2tx+t2-1=0的两个根中的一个根在（-2，0）内，另一个根在（1，2）内，则实数t的取值范围是（0，1）．分析 令f（x）=x2-2tx+t2-1，若方程x2-2tx+t2-1=0的两个根中的一个根在（-2，0）内，另一个根在（1，2）内，即$\left\{\begin{array}{l}f（-2）＞0\\ f（0）＜0\\ f（1）＜0\\ f（2）＞0\end{array}\right.$，解得答案．
解答 解：令f（x）=x2-2tx+t2-1，
若方程x2-2tx+t2-1=0的两个根中的一个根在（-2，0）内，另一个根在（1，2）内，
则$\left\{\begin{array}{l}f（-2）＞0\\ f（0）＜0\\ f（1）＜0\\ f（2）＞0\end{array}\right.$，即$\left\{\begin{array}{l}{t}^{2}+4t+3＞0\\{t}^{2}-1＜0\\{t}^{2}-2t＜0\\{t}^{2}-4t+3＞0\end{array}\right.$，
解得：t∈（0，1），
故答案为：（0，1）．
点评 本题考查的知识点是二次函数的性质，函数的零点与方程的根，难度中档．
练习册系列答案
相关题目
16．在△ABC中，$\overrightarrow{BA}$=（cos16°，sin16°），$\overrightarrow{BC}$=（2sin29°，2cos29°），则△ABC面积为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{4}$ |
13．已知集合A={x|x≤3，x∈R}，B={x|x-1≥0，x∈N}，则A∩B=（ ）
| A． | {0，1} | B． | {0，1，2} | C． | {2，3} | D． | {1，2，3} |
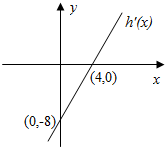已知二次函数h（x）=ax2+bx+2，其导函数y=h′（x）的图象如图，f（x）=6lnx+h（x）．