题目内容
已知长方形ABCD,AB=3,BC=2,E为BC中点,P为AB上一点
(1)利用向量知识判定点P在什么位置时,∠PED=450;
(2)若∠PED=450,求证:P、D、C、E四点共圆。
(1)利用向量知识判定点P在什么位置时,∠PED=450;
(2)若∠PED=450,求证:P、D、C、E四点共圆。
(Ⅰ) 点P为靠近点A的AB三等分处 (Ⅱ) 见解析
:(Ⅰ)利用坐标系可以确定点P位置建立平面直角坐标系则C(2,0),D(2,3),E(1,0)设P(0,y)∴ 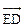 =(1,3),
=(1,3),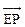 =(-1,y)∴
=(-1,y)∴ 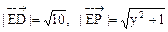
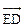 ·
·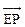 =3y-1代入cos450=
=3y-1代入cos450=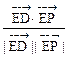 解之得
解之得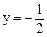 (舍),或y=2
(舍),或y=2
∴ 点P为靠近点A的AB三等分处
(Ⅱ) 当∠PED=450时,由(1)知P(0,2) ∴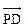 =(2,1),
=(2,1),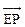 =(-1,2)
=(-1,2)
∴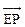 ·
·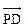 =0∴ ∠DPE=900又∠DCE=900∴ D、P、E、C四点共圆
=0∴ ∠DPE=900又∠DCE=900∴ D、P、E、C四点共圆
说明:利用向量处理几何问题一步要骤为:①建立平面直角坐标系;②设点的坐标;③求出有关向量的坐标;④利用向量的运算计算结果;⑤得到结论。
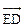 =(1,3),
=(1,3),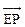 =(-1,y)∴
=(-1,y)∴ 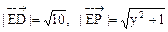
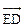 ·
·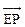 =3y-1代入cos450=
=3y-1代入cos450=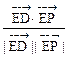 解之得
解之得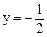 (舍),或y=2
(舍),或y=2∴ 点P为靠近点A的AB三等分处
(Ⅱ) 当∠PED=450时,由(1)知P(0,2) ∴
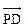 =(2,1),
=(2,1),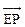 =(-1,2)
=(-1,2)∴
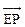 ·
·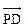 =0∴ ∠DPE=900又∠DCE=900∴ D、P、E、C四点共圆
=0∴ ∠DPE=900又∠DCE=900∴ D、P、E、C四点共圆说明:利用向量处理几何问题一步要骤为:①建立平面直角坐标系;②设点的坐标;③求出有关向量的坐标;④利用向量的运算计算结果;⑤得到结论。

练习册系列答案
相关题目
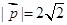 ,
,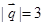 ,
,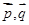 的夹角为
的夹角为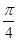 ,如图,若
,如图,若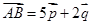 ,
,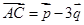 ,
,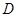 为
为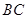 的中点,则
的中点,则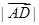 为( ).
为( ).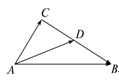
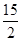
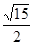
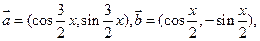 若
若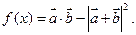
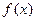 的单调减区间;
的单调减区间;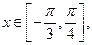 求函数
求函数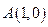 ,直线
,直线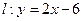 ,点
,点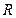 是直线
是直线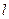 上的一点,若
上的一点,若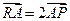 ,求点
,求点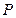 的轨迹方程.
的轨迹方程. m,一艘船从
m,一艘船从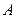 处出发到河对岸.已知船的速度
处出发到河对岸.已知船的速度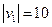 km/h,水流速度
km/h,水流速度 km/h.要使船行驶的时间最短,那么船行驶的距离与合速度的比值必须最小.此时我们分三种情况讨论:
km/h.要使船行驶的时间最短,那么船行驶的距离与合速度的比值必须最小.此时我们分三种情况讨论: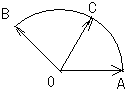
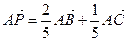 ,
,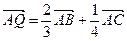 ,则△ABP的面积与△ABQ的面积之比( )
,则△ABP的面积与△ABQ的面积之比( )




 和
和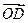 的坐标;
的坐标; 的夹角的大小.
的夹角的大小.
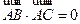 ,
, 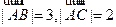 ,则
,则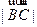 =( )
=( ) 
 B.
B. 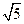 C.
C. 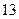 D.
D.