题目内容
3.设函数$f(x)=4sin(wx+\frac{π}{3})(w>0)$的最小正周期为π.(1)求w的值及函数f(x)的对称轴方程;
(2)设向量$\overrightarrow a=(-1,f(x)),\overrightarrow b=(f(-x),1),g(x)=\overrightarrow a•\overrightarrow b$,求函数g(x)在区间$[\frac{π}{8},\frac{π}{3}]$上的最大值和最小值.
分析 (1)根据三角函数的周期公式即可求w的值及函数f(x)的对称轴方程;
(2)根据向量的数量积将函数g(x)进行化简,结合三角函数的最值性进行求解即可.
解答 解:(1)∵$f(x)=4sin(wx+\frac{π}{3})(w>0)$的最小正周期为π.
∴$\frac{2π}{ω}=π$,解得ω=2,
则f(x)=4sin(2x+$\frac{π}{3}$),
由2x+$\frac{π}{3}$=$\frac{π}{2}+$kπ,k∈Z.
解得x=$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z.
即函数的对称轴方程为x=$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z.
(2)设向量$\overrightarrow a=(-1,f(x)),\overrightarrow b=(f(-x),1),g(x)=\overrightarrow a•\overrightarrow b$,
则g(x)=-f(-x)+f(x)=4sin(2x+$\frac{π}{3}$)-4sin(-2x+$\frac{π}{3}$)=4sin(2x+$\frac{π}{3}$)+4sin(2x-$\frac{π}{3}$)
=4sin2xcos$\frac{π}{3}$=2sin2x,
若x∈$[\frac{π}{8},\frac{π}{3}]$,则2x∈[$\frac{π}{4}$,$\frac{2π}{3}$],
故当2x=$\frac{π}{2}$,即x=$\frac{π}{4}$时,函数g(x)取得最大值为g($\frac{π}{4}$)=2,
当2x=$\frac{π}{4}$,即x=$\frac{π}{8}$时,函数g(x)取得最小值为g($\frac{π}{8}$)=2sin$\frac{π}{4}$=2×$\frac{\sqrt{2}}{2}=\sqrt{2}$.
点评 本题主要考查三角函数的性质,根据三角函数的周期公式求出函数的解析式以及利用向量的数量积公式是解决本题的关键.

| A. | $\frac{1}{4}$ | B. | $\frac{7}{16}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{4}$ |
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
| A. | sinα>0,cosα>0,tanα>0 | B. | sinα>0,cosα<0,tanα<0 | ||
| C. | sinα<0,cosα<0,tanα>0 | D. | sinα<0,cosα>0,tanα<0 |
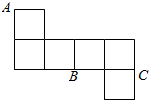
| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
| A. | (-∞,-$\frac{1}{4}$] | B. | (-∞,$\frac{1}{4}$] | C. | [-$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |