题目内容
17.在一批棉花中抽测了60根棉花的纤维长度,结果如下(单位:mm):82 202 352 321 25 293 293 86 28 206
323 355 357 33 325 113 233 294 50 296
115 236 357 326 52 301 140 328 238 358
58 255 143 360 340 302 370 343 260 303
59 146 60 263 170 305 380 346 61 305
175 348 264 383 62 306 195 350 265 385
作出这个样本的频率分布直方图(在对样本数据分组时,可试用不同的分组方式,然后从中选择一种较为适合的分组方法).棉花的纤维长度是棉花质量的重要指标,你能从图中分析出这批棉花的质量状况吗?
分析 按照画频率分布直方图的基本步骤:(1)求极差,(2)确定组距与组数,(3)列频率分布表,(4)画频率分布直方图,画出图形;
根据频率分布直方图,得出频率估计与分析.
解答 解:(1)求极差,385-25=360;
(2)确定组距与组数,$\frac{360}{6}$=60,
分6组,组距为60;
(3)列频率分布表,如下表;
| 分组 | 频数 | 频率 |
| [25,85) | 11 | $\frac{11}{60}$ |
| [85,145) | 5 | $\frac{1}{12}$ |
| [145,205) | 5 | $\frac{1}{12}$ |
| [205,265) | 8 | $\frac{2}{15}$ |
| [265,325) | 13 | $\frac{13}{60}$ |
| [325,385] | 18 | $\frac{3}{10}$ |
| 总计 | 60 | 1.00 |
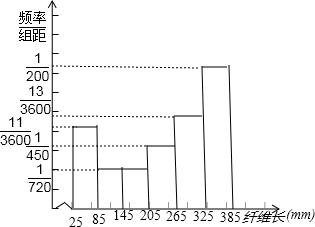
根据频率分布直方图,得;
该种棉花的纤维长度分布在25~385mm之间,其中纤维长度在265~385mm的棉花占一半多($\frac{31}{60}$).
点评 本题考查了画频率分布直方图的应用问题,也考查了利用频率分布直方图进行频率分析与估计的应用问题,是基础题目.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
7. 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | B. | -$\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ |
8.若将如图的展开图还原成成正方体,则∠ABC的度数为( )
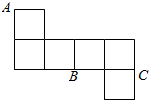

| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
12.当x>0时,不等式$\frac{x}{{x}^{2}+1}$≤1-2p恒成立,则实数p的取值范围是( )
| A. | (-∞,-$\frac{1}{4}$] | B. | (-∞,$\frac{1}{4}$] | C. | [-$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |