题目内容
(本小题满分12分) 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=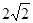 ,SA=SB=
,SA=SB=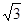 。
。
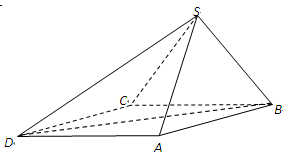
(1)证明:SA⊥BC;
(2)求直线SD与平面SAB所成角的大小;
(3)求二面角D-SA-B的大小.
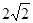 ,SA=SB=
,SA=SB=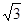 。
。
(1)证明:SA⊥BC;
(2)求直线SD与平面SAB所成角的大小;
(3)求二面角D-SA-B的大小.
(1)见解析;(2)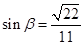 ;(3)
;(3)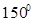 .
.
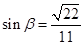 ;(3)
;(3)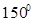 .
.(1)通过面面垂直找到与底面垂直的线SO,然后建立空间直角坐标系,利用向量法证明两条直线垂直;(2)利用向量法把直线与平面所成的角转化为已知直线向量与平面法向量的夹角,利用数量积知识求解夹角即可;(3)先求出两个平面的法向量,然后把二面角的大小问题转化为求两法向量的夹角问题。
证明:(1)作 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面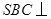 底面
底面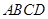 ,得
,得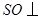 平
平
面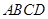 . 因为
. 因为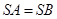 ,所以
,所以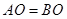 .
.
又 ,
, 为等腰直角三角形,
为等腰直角三角形,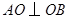 .如图,以
.如图,以 为坐标原点,
为坐标原点,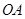
为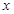 轴正向,建立直角坐标系
轴正向,建立直角坐标系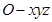
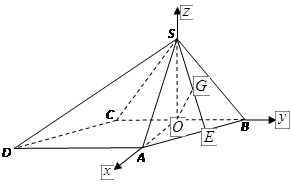
 ,
,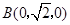 ,
, ,
, ,
, ,
,
 ,
,
 ,…所以
,…所以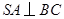 .………………………4分
.………………………4分
(2)取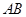 中点
中点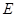 ,
,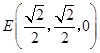 ,
,
连结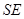 ,取
,取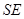 中点
中点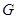 ,连结
,连结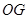 ,
,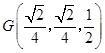 .
.
 ,
,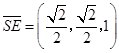 ,
,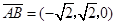 .
.
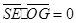 ,
,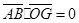 ,
,
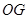 与平面
与平面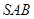 内两条相交直线
内两条相交直线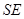 ,
,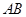 垂直.
垂直.
所以 平面
平面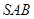 ,
, 与
与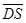 的夹角记为
的夹角记为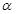 ,
, 与平面
与平面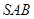 所成的角记为
所成的角记为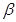 ,则
,则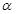 与
与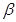 互余.
互余.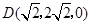 ,
, .
.
 ,所以
,所以 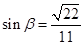 ,……………8分
,……………8分
(3)由上知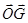 为平面SAB的法向量,
为平面SAB的法向量, 。易得
。易得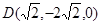
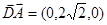 ,
,
同理可求得平面SDA的一个法向量为 ………10分
………10分
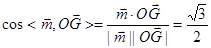
由题知所求二面角为钝二面角,故二面角D-SA-B的大小为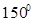 。………12分
。………12分
证明:(1)作
 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面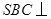 底面
底面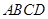 ,得
,得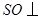 平
平面
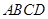 . 因为
. 因为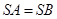 ,所以
,所以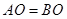 .
.又
 ,
, 为等腰直角三角形,
为等腰直角三角形,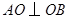 .如图,以
.如图,以 为坐标原点,
为坐标原点,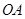
为
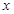 轴正向,建立直角坐标系
轴正向,建立直角坐标系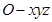

 ,
,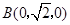 ,
, ,
, ,
, ,
, ,
,  ,…所以
,…所以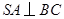 .………………………4分
.………………………4分(2)取
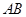 中点
中点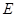 ,
,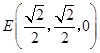 ,
,连结
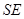 ,取
,取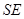 中点
中点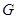 ,连结
,连结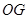 ,
,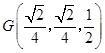 .
. ,
,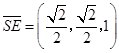 ,
,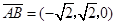 .
.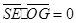 ,
,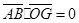 ,
,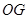 与平面
与平面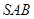 内两条相交直线
内两条相交直线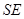 ,
,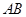 垂直.
垂直. 所以
 平面
平面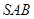 ,
, 与
与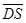 的夹角记为
的夹角记为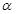 ,
, 与平面
与平面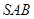 所成的角记为
所成的角记为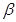 ,则
,则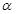 与
与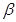 互余.
互余.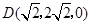 ,
, .
. ,所以
,所以 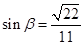 ,……………8分
,……………8分(3)由上知
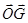 为平面SAB的法向量,
为平面SAB的法向量, 。易得
。易得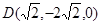
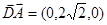 ,
,
同理可求得平面SDA的一个法向量为
 ………10分
………10分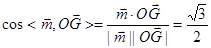
由题知所求二面角为钝二面角,故二面角D-SA-B的大小为
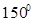 。………12分
。………12分
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
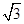 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.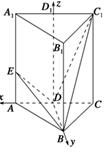
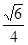 ,求二面角E-AF-C的余弦值.
,求二面角E-AF-C的余弦值.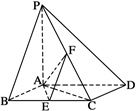
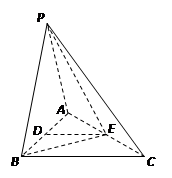
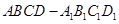 是正方体,其中
是正方体,其中
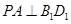 ;
;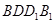 所成的锐二面角
所成的锐二面角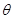 的余弦值;
的余弦值;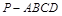 的底面
的底面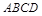 是正方形,侧棱
是正方形,侧棱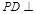 底面
底面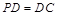 ,
,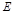 是
是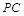 的中点.
的中点.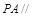 平面
平面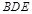 ;
;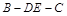 的余弦值.
的余弦值.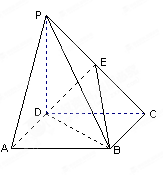
 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱 面
面 是
是 的中点.
的中点. ;(2)求证:
;(2)求证: ∥平面
∥平面

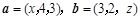 ,且
,且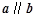 ,则
,则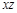 等于( )
等于( )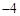
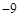
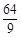
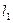 的方向向量为
的方向向量为 ,直线
,直线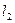 的方向向量为
的方向向量为 ,那么
,那么