Question

【题目】已知函数f（x）=log2（5﹣x）﹣log2（5+x）+1+m
（1）若f（x）是奇函数，求实数m的值．
（2）若m=0，则是否存在实数x，使得f（x）＞2？若存在，求出x的取值范围；若不存在，请说明理由．

Answer 1

【答案】
（1）解：∵f（x）为奇函数，∴f（﹣x）+f（x）=0对定义域中的任意x都成立，

∴log2（5+x）﹣log2（5﹣x）+log2（5﹣x）﹣log2（5+x）+2（1+m）=0，

∴m=﹣1

（2）解：假设存在实数x，使得f（x）＞2，

∴log2（5﹣x）﹣log2（5+x）+1＞2，

∴log2（5﹣x）＞log2（5+x）+1，

∴log2（5﹣x）＞log2（5+x）+log22，

∴log2（5﹣x）＞log22（5+x），

∴ ，

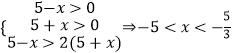∴存在实数 ，使得f（x）＞2

【解析】1、本题考查的是奇函数的定义，f（x）为奇函数，f（﹣x）+f（x）=0，由定义可得。
2、本题考查的是对数的运算性质，(1)(2),由对数的单调性可得不等式组可得 5 < x < ,使得f（x）＞2.