题目内容
【题目】在四棱锥P﹣ABCD中,AB⊥AD,CD⊥AD,PA⊥平面ABCD,PA=AD=CD=2AB=2,M为PC的中点. (Ⅰ)求证:BM∥平面PAD;
(Ⅱ)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定点N的位置;若不存在,请说明理由.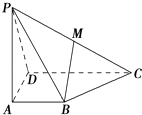
【答案】证明:(Ⅰ)如图,取PD中点E,连接EM、AE, ∴EM ![]()
![]() CD,而AB
CD,而AB ![]()
![]() CD,∴EM∥AB,
CD,∴EM∥AB,
∴四边形ABME是平行四边形,∴BM∥AE
∵AE平面ADP,BM平面ADP,
∴BM∥平面PAD.
(Ⅱ)解:∵PA⊥平面ABCD,
∴PA⊥AB,而AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,∴AB⊥PD
∵PA=AD,E是PD的中点,
∴PD⊥AE,AB∩AE=A,∴PD⊥平面ABME
作MN⊥BE,交AE于点N,则MN⊥平面PBD
由题意知△BME∽△MEN,而BM=AE= ![]() ,EM=
,EM= ![]() CD=1,
CD=1,
由 ![]() =
= ![]() ,得EN=
,得EN= ![]() =
= ![]() =
= ![]() ,
,
∴AN= ![]() ,即点N为AE的中点.
,即点N为AE的中点. 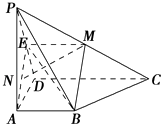
【解析】(Ⅰ)取PD中点E,连接EM、AE,由已知得四边形ABME是平行四边形,由此能证明BM∥平面PAD.(Ⅱ)由已知PA⊥AB,AB⊥AD,从而AB⊥平面PAD,进而AB⊥PD,由此得到PD⊥平面ABME,作MN⊥BE,交AE于点N,则MN⊥平面PBD,从而求出点N为AE的中点.
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的性质是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目