题目内容
14.定义在R上的奇函数f(x)的导函数满足f′(x)<f(x),且f(x)•f(x+3)=-1,若f(2015)=-e,则不等式f(x)<ex的解集为{0}∪(1,+∞)..分析 由题意知,f(,1)=1,再令g(x)=(x∈R),从而求导g′(x)=<0,从而可判断y=g(x)单调递减,从而可得到不等式的解集
解答 解:∵f(x)•f(x+3)=-1,
∴f(x+3)=-,
∴f(x+6)=-=f(x),
即f(x)的周期为6,
∵f(2015)=-e,
∴f(2015)=f(-1)=-e,
∵定义在R上的奇函数f(x),
∴f(1)=e,
①f(x)≠0时,令g(x)=,g′(x)=,
∵f′(x)<f(x),
∴g′(x)=<0.
即g(x)单调递减,
g(1)==1,
∵g(x)<1=g(1),
∴x>1,
∴不等式f(x)<ex的解集为(1,+∞)
②∵x=0时,f(0)=0<e0=1
∴x=0时,不等式成立.
故答案为{0}∪(1,+∞)
点评 本题考查了导数的综合应用及函数的性质的应用,构造函数的思想,阅读分析问题的能力,属于中档题

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.下列四个命题中正确命题的是( )
| A. | 学校抽取每个班级座号为21-30号的同学检查作业完成情况,这是分层抽样 | |
| B. | 可以通过频率分布直方图中最高小矩形的高来估计这组数据的众数 | |
| C. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=1-p | |
| D. | 在散点图中,回归直线至少经过一个点 |
3.若集合A={x|2>1},集合B={x|y=lg},则A∩B=( )
| A. | {x|-5<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<-1} | D. | {x|-5<x<-1} |

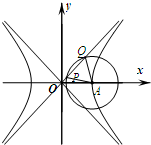 如图,已知双曲线C:
如图,已知双曲线C: