题目内容
6.合肥八中模拟联合国协会共有三个小组:中文组,英文组,辩论组,现有12名新同学(其中3名为男同学)被平均分配到三个小组.(Ⅰ)求男同学甲被分到中文组,其他2名男同学被分到另外两个不同小组的概率;
(Ⅱ)若男同学所在的小组个数为X,求X的概率分布列及数学期望.
分析 (1)男同学甲被分到中文组,且其他2名男同学被分别分到另外2个不同小组共有${C}_{9}^{3}{C}_{2}^{1}{C}_{6}^{3}$种分法,12名同学被分到3个小组共有${C}_{12}^{4}{C}_{8}^{4}$种分法,求得概率
(2)求得随机变量X的可能值的概率,并求出分布列.
解答 解:(1)男同学甲被分到中文组,且其他2名男同学被分别分到另外2个不同小组共有${C}_{9}^{3}{C}_{2}^{1}{C}_{6}^{3}$种分法,
12名同学被分到3个小组共有${C}_{12}^{4}{C}_{8}^{4}$种分法,∴P=$\frac{16}{165}$,
(2)X的取值为1,2,3,
P(X=1)=$\frac{3}{55}$,P(X=2)=$\frac{36}{55}$,P(X=3)=$\frac{16}{55}$,
故X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{3}{55}$ | $\frac{36}{55}$ | $\frac{16}{55}$ |
点评 本题主要考查古典概型及其概率计算以及随机变量的期望,属于中档题型.

练习册系列答案
相关题目
16.执行如图所示的程序框图,若a=1,b=2,则输出的结果是( )
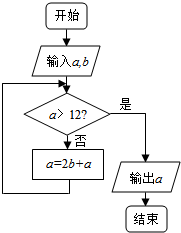

| A. | 9 | B. | 11 | C. | 13 | D. | 15 |
15.执行如图所示的程序框图,会输出一列数,则这个数列的第3项是( )


| A. | 870 | B. | 30 | C. | 6 | D. | 3 |
16.已知x、y均为实数,记max{x,y}=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,min{x,y}=$\left\{\begin{array}{l}{y,x≥y}\\{x,x<y}\end{array}\right.$.若i表示虚数单位,且a=x1+y1i,b=x2+y2i,x1,y1,x2,y2∈R,则( )
| A. | min{|a+b|,|a-b|}≤min{|a|,|b|} | B. | max{|a+b|,|a-b|}≤max{|a|,|b|} | ||
| C. | min{|a+b|2,|a-b|2}≥|a|2+|b|2 | D. | max{|a+b|2,|a-b|2}≥{|a|2+|b|2 |
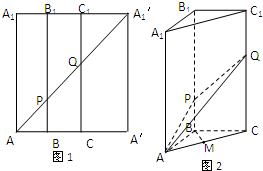 如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:
如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中: