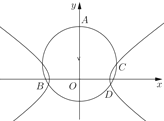
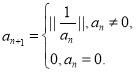题目内容
【题目】如图,已知圆![]() :
:![]() (
(![]() )和双曲线
)和双曲线![]() :
:![]() (
(![]() ),记
),记![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴负半轴的公共点分别为
轴负半轴的公共点分别为![]() 、
、![]() ,又记
,又记![]() 与
与![]() 在第一、第四象限的公共点分别为
在第一、第四象限的公共点分别为![]() 、
、![]() .
.
(1)若![]() ,且
,且![]() 恰为
恰为![]() 的左焦点,求
的左焦点,求![]() 的两条渐近线的方程;
的两条渐近线的方程;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)若![]() 恰为
恰为![]() 的左焦点,求证:在
的左焦点,求证:在![]() 轴上不存在这样的点
轴上不存在这样的点![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)依据圆的方程求出点B坐标,进而求出![]() ,得到双曲线的渐近线方程;
,得到双曲线的渐近线方程;
(2)联立圆与双曲线方程,得到关于![]() 的方程,利用根与系数的关系求出
的方程,利用根与系数的关系求出![]() ,再根据
,再根据![]() 建立等式,求出实数
建立等式,求出实数![]() ;(3)先证明出AC的长为定值,再根据三角不等式说明,这样的点
;(3)先证明出AC的长为定值,再根据三角不等式说明,这样的点![]() 不存在。
不存在。
(1)当![]() 时,圆
时,圆![]() :
:![]() ,所以点B的坐标为
,所以点B的坐标为![]() ,
,
即有![]() ,
,![]() ,故
,故![]() 的两条渐近线的方程为
的两条渐近线的方程为![]() ;
;
(2)当![]() 时,圆
时,圆![]() :
:![]() ,
,![]() :
:![]() ,
,
联立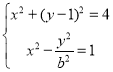 得,
得,![]() ,设
,设![]()
所以![]() ,因为点A的坐标是(0,3),由
,因为点A的坐标是(0,3),由![]() 得
得
![]() ,
,![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
解得![]() ,代入
,代入![]() ,解得
,解得![]() ,
,![]()
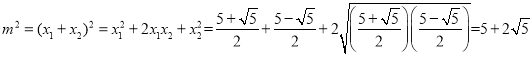
故![]() 。
。
(3)由题意知,点A的坐标是![]() ,
, ![]() ,
,
由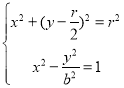 得,
得,![]() ,
,
![]() ,
,![]()
所以用求根公式求得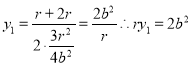 ,
,
因为![]() ,所以
,所以![]() ,
, ![]()
即![]() ,故
,故![]() ,又
,又![]() ,
,
故在![]() 轴上不存在这样的点
轴上不存在这样的点![]() ,使得
,使得![]() .
.

练习册系列答案
相关题目