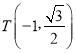题目内容
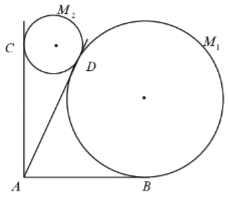
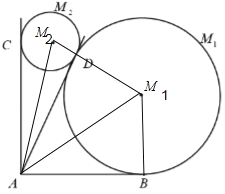
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
【答案】(1)34.6米,16.1米;(2)263.8千元.
【解析】
(1)利用切线的性质即可得出圆的半径;
(2)设∠BAD=2α,则总造价y=0.82π60tanα+0.92π60tan(45°﹣α),化简,令1+tanα=x换元,利用基本不等式得出最值.
(1)连结M1M2,AM1,AM2,
∵圆M1与AB,AD相切于B,D,圆M2与AC,AD分别相切于点C,D,
∴M1,M2⊥AD,∠M1AD=![]() ∠BAD=
∠BAD=![]() ,∠M2AD=
,∠M2AD=![]() ,
,
∴M1B=ABtan∠M1AB=60×![]() =20
=20![]() ≈34.6(米),
≈34.6(米),
∵tan![]() =
=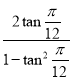 =
=![]() ,∴tan
,∴tan![]() =2﹣
=2﹣![]() ,
,
同理可得:M2D=60×tan![]() =60(2﹣
=60(2﹣![]() )≈16.1(米).
)≈16.1(米).
(2)设∠BAD=2α(0<α<![]() ),由(1)可知圆M1的半径为60tanα,圆M2的半径为
),由(1)可知圆M1的半径为60tanα,圆M2的半径为
60tan(45°﹣α),
设观景步道总造价为y千元,则y=0.82π60tanα+0.92π60tan(45°﹣α)=96πtanα+108π![]() ,
,
设1+tanα=x,则tanα=x﹣1,且1<x<2.
∴y=96π(x﹣1)+108π(![]() )=12π(8x+
)=12π(8x+![]() ﹣17)≥84π≈263.8,
﹣17)≥84π≈263.8,
当且仅当8x=![]() 即x=
即x=![]() 时取等号,
时取等号,
当x=![]() 时,tanα=
时,tanα=![]() ,∴α≈26.6°,2α≈53.2°.
,∴α≈26.6°,2α≈53.2°.
∴当∠BAD为53.2°时,观景步道造价最低,最低造价为263.8千元.

练习册系列答案
相关题目