题目内容
7．用描述法表示集合：（1）小于100的自然数组成的集合A={x|x＜100，且x∈N}；
（2）大于2而小于5的实数组成的集合R={x|2＜x＜5，x∈R}．
分析 根据集合的表示法，根据题意描述即可．
解答 解（1）小于100的自然数组成的集合A={x|x＜100，且x∈N}，
（2）大于2而小于5的实数组成的集合R={x|2＜x＜5，x∈R}，
故答案为：（1）{x|x＜100，且x∈N}，（2）{x|2＜x＜5，x∈R}．
点评 此题是个基础题．本题考查描述法表示集合，抓住描述法的特征表示即可．
练习册系列答案
相关题目
18．若a=log2x，b=$\frac{2}{x}$，则“a＞b”是“x＞1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
15．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}-1（x≤0）}\\{f（x-1）（x＞0）}\end{array}\right.$，若函数y=f（x）-x-$\frac{a}{2}$恰有两个不同的零点，则实数a的取值范围是（ ）
| A． | （0，2） | B． | （-∞，2） | C． | （-∞，2] | D． | [0，+∞） |
12．已知f（x）、g（x）、h（x）均为一次函数．若对实数x满足：
|f（x）|-|g（x）|+h（x）=$\left\{\begin{array}{l}{-2，x＜-1}\\{7x+5，-1≤x＜0}\\{-4x+5，x≥0}\end{array}\right.$，h（x）的解析式为．
|f（x）|-|g（x）|+h（x）=$\left\{\begin{array}{l}{-2，x＜-1}\\{7x+5，-1≤x＜0}\\{-4x+5，x≥0}\end{array}\right.$，h（x）的解析式为．
| A． | 2x-$\frac{3}{2}$ | B． | -2x-$\frac{3}{2}$ | C． | 2x+$\frac{3}{2}$ | D． | -2x+$\frac{3}{2}$ |
16．
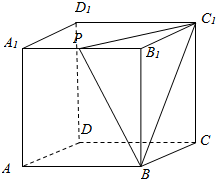如图，在棱长为2的正方体ABCD-A1B1C1D1中，A1B1的中点是P，过点A1作截面PBC1平行的截面，则该截面的面积为（ ）
如图，在棱长为2的正方体ABCD-A1B1C1D1中，A1B1的中点是P，过点A1作截面PBC1平行的截面，则该截面的面积为（ ）| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | 2$\sqrt{6}$ | D． | 4 |