Question

【题目】设函数f（x）＝x3＋ax2＋bx＋1的导数满足，其中常数a，b∈R.

（1）求曲线y＝f（x）在点（1，f（1））处的切线方程；

（2）设，求函数g（x）的极值.

Answer 1

【答案】(1)；(2)见解析

【解析】

（1）求出导函数f′（x）=3x2+2ax+b，利用约束条件列出方程，求出a，b，求出切点坐标以及斜率，然后求解切线方程;（2）化简g（x）=（3x2﹣3x﹣3）e﹣x，求出导数，求出极值点，判断导函数的符号，推出函数的单调性，求解函数的极值即可．

（1）∵f（x）＝x3＋ax2＋bx＋1，∴f′（x）＝3x2＋2ax＋b，

则解得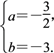

∴f（x）＝x3－x2－3x＋1，∴f（1）＝－，f′（1）＝－3，

∴y＝f（x）在（1，f（1））处的切线方程为

y－＝－3（x－1），即6x＋2y－1＝0；

（2）由（1）知g（x）＝（3x2－3x－3）e－x，

∴g′（x）＝（－3x2＋9x）e－x，

令g′（x）＝0，即（－3x2＋9x）e－x＝0，得x＝0或x＝3，

当x∈（－∞，0）时，g′（x）<0，

故g（x）在（－∞，0）上单调递减.

当x∈（0,3）时，g′（x）>0，故g（x）在（0,3）上单调递增.

当x∈（3，＋∞）时，g′（x）<0，

故g（x）在（3，＋∞）上单调递减.

从而函数g（x）在x＝0处取得极小值g（0）＝－3，

在x＝3处取得极大值g（3）＝15e－3.