��Ŀ����
����Ŀ��ijУ������ѧ�����������ԺԿ����ijɼ�����ͳ�ƣ������ɼ���������90�֣�����150�֣������ɼ������·�ʽ�ֳ����飬��һ��[90��100�����ڶ���[100��110����������[140��150]��ͼ��1��Ϊ��Ƶ�ʷֲ�ֱ��ͼ��һ���֣������ġ��塢������������γɵȲ����У��ҵ�������4�ˣ� �����벹������Ƶ�ʷֲ�ֱ��ͼ���������������ݵ�ƽ����M��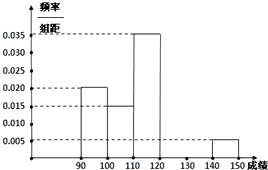
������������120�ֵ�ͬѧ���������������140�ֵ�ͬѧΪ����ѡ�֣��������2��2
������������д�ո����ݣ������ж��Ƿ���99%�İ�����Ϊ�����������ͬѧ
��Ϊ����ѡ����ר����ѵ�йء���
| [140��150] | �ϼ� | |
�μ���ѵ | 5 | 8 | |
δ�μ���ѵ | |||
�ϼ� | 4 |
���� ![]()
P��K2��k0�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡��⣺��������ģ������Ƶ�ʷֱ�Ϊx��y����2y=x+0.005��10�� x+y=1����0.005+0.015+0.02+0.035����10��
�ɢ٢ڽ��x=0.15��y=0.10
�Ӷ��ó�ֱ��ͼ����ͼ��ʾ��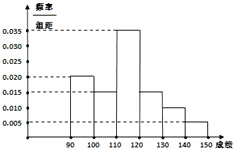
M=95��0.2+105��0.15+115��0.35+125��0.15+135��0.1+145��0.05=114.5
���������⣬�����������Ϊ ![]() ��������д���������£�
��������д���������£�
[120��140�� | [140��150] | �ϼ� | |
�μ���ѵ | 5 | 3 | 8 |
δ�μ���ѵ | 15 | 1 | 16 |
�ϼ� | 20 | 4 | 24 |
���� ![]() ����û��99%�İ�����Ϊ�����������ͬѧ��Ϊ����ѡ����ר����ѵ�й�
����û��99%�İ�����Ϊ�����������ͬѧ��Ϊ����ѡ����ר����ѵ�й�
��������������������Ƶ�ʷֲ�ֱ��ͼ���г�����x��y�ķ��̣��������̣��õ������飬�ⷽ����õ�Ҫ���Ƶ�ʣ���������Ƶ�ʷֲ�ֱ��ͼ�����M��ֵ���������ֻ�����������������õ��������ĸ���λ�õ����ݣ������������������������е����ݣ����������������Ĺ۲�ֵ�Ĺ�ʽ�����۲�ֵ���õ�û��99%�İ�����Ϊ�����������ͬѧ��Ϊ����ѡ����ר����ѵ�йأ�
�����㾫�����������⣬������Ҫ�˽�Ƶ�ʷֲ�ֱ��ͼ(Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ)��

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�