题目内容
【题目】已知函数f(x)=ax3+bx2+2x在x=﹣1处取得极值,且在点(1,f(1))处的切线的斜率为2. (Ⅰ)求a,b的值:
(Ⅱ)若关于x的方程f(x)+x3﹣2x2﹣x+m=0在[ ![]() ,2]上恰有两个不相等的实数根,求实数m的取值范围.
,2]上恰有两个不相等的实数根,求实数m的取值范围.
【答案】解:(I)∵函数f(x)=ax3+bx2+2x在x=﹣1处取得极值, ∴f'(﹣1)=3a﹣2b+2=0
又∵在点(1,f(1)处的切线的斜率为2.
f'(1)=3a+2b+2=2
解得a=﹣ ![]() ,b=
,b= ![]()
0在(1,2)内有根.(
(II)由(I)得方程f(x)+x3﹣2x2﹣x+m=0可化为:![]()
令g(x)= ![]()
则g'(x)=2x2﹣3x+1
∵当x∈[ ![]() ,1]时,g'(x)≤0,当x∈[1,2]时,g'(x)≥0,
,1]时,g'(x)≤0,当x∈[1,2]时,g'(x)≥0,
故g(x)= ![]() 在[
在[ ![]() ,1]上单调递减,在[1,2]上单调递增,
,1]上单调递减,在[1,2]上单调递增,
若关于x的方程f(x)+x3﹣2x2﹣x+m=0在[ ![]() ,2]上恰有两个不相等的实数根,
,2]上恰有两个不相等的实数根,
则 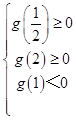
解得: ![]()
【解析】(I)根据已知中函数f(x)=ax3+bx2+2x在x=﹣1处取得极值,且在点(1,f(1)处的切线的斜率为2.我们易得f'(﹣1)=0,f'(1)=2,由此构造关于a,b的方程,解方程即可得到答案.(II)根据(I)的结论我们易化简关于x的方程f(x)+x3﹣2x2﹣x+m=0,构造函数g(x)= ![]() 分析函数的单调性后,我们可将关于x的方程f(x)+x3﹣2x2﹣x+m=0在[
分析函数的单调性后,我们可将关于x的方程f(x)+x3﹣2x2﹣x+m=0在[ ![]() ,2]上恰有两个不相等的实数根,转化为不等式问题,解关于m的不等式组,即可求出实数m的取值范围.
,2]上恰有两个不相等的实数根,转化为不等式问题,解关于m的不等式组,即可求出实数m的取值范围.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值的理解,了解极值反映的是函数在某一点附近的大小情况.
在这个区间单调递减,以及对函数的极值的理解,了解极值反映的是函数在某一点附近的大小情况.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案