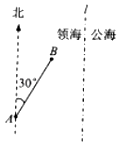
��Ŀ����
����Ŀ����֪Բ![]() ����
����![]() ��ֱ��
��ֱ��![]() .
.
��1������Բ![]() ����������ֱ��
����������ֱ��![]() ��ֱ��ֱ�߷�����
��ֱ��ֱ�߷�����
��2����ֱ��![]() ����
����![]() Ϊ����ԭ�㣩�����ڶ���
Ϊ����ԭ�㣩�����ڶ���![]() ����ͬ�ڵ�
����ͬ�ڵ�![]() �������㣺����Բ
�������㣺����Բ![]() ����һ��
����һ��![]() ������
������![]() Ϊһ�����������������������ĵ�
Ϊһ�����������������������ĵ�![]() ������.
������.
���𰸡�(1)![]() ��(2)�𰸼�����.
��(2)�𰸼�����.
�����������������
��1��������ֱ�߷���Ϊ![]() ������Բ�ĵ�ֱ�ߵľ�����ڰ뾶�ɵù���b�ķ��̣��ⷽ�̿ɵ�
������Բ�ĵ�ֱ�ߵľ�����ڰ뾶�ɵù���b�ķ��̣��ⷽ�̿ɵ�![]() ��������ֱ�߷���Ϊ
��������ֱ�߷���Ϊ![]()
��2������1��������������ĵ�![]() ��������ɵ�
��������ɵ�![]() ����
����![]() ��Ȼ��֤��
��Ȼ��֤��![]() Ϊ����
����![]() ����.
����.
����2��������������ĵ�![]() ��ʹ��
��ʹ��![]() Ϊ����
����![]() ����
����![]() ���ݴ˵õ�����
���ݴ˵õ�����![]() �ķ����飬��ⷽ����ɵô��ڵ�
�ķ����飬��ⷽ����ɵô��ڵ�![]() ����Բ
����Բ![]() ����һ��
����һ��![]() ������
������![]() ����
����![]() .
.
���������
��1��������ֱ�߷���Ϊ![]() ����
����![]() ��
��
��ֱ����Բ���У���![]() ����
����![]() ��
��
������ֱ�߷���Ϊ![]()
��2������1��������������ĵ�![]() ��
��
��![]() ΪԲ
ΪԲ![]() ��
��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
��![]() ΪԲ
ΪԲ![]() ��
��![]() ���ҽ���
���ҽ���![]() ʱ��
ʱ��![]() ��
��
�����⣬![]() ����ã�
����ã�![]() ����ȥ������
����ȥ������![]() .
.
����֤����![]() ����Բ
����Բ![]() ����һ��
����һ��![]() ������
������![]() Ϊһ����.
Ϊһ����.
��![]() ����
����![]() ��
��
��![]()
![]()
![]() ��
��
�Ӷ�![]() Ϊ����.
����.
����2��������������ĵ�![]() ��ʹ��
��ʹ��![]() Ϊ����
����![]() ����
����![]() ��
��
��![]() ����
����![]() ����ã�
����ã�
![]() ����
����
![]() ��
��![]() �������
�������
��![]() �����
����� ��
��![]() ����ȥ����
����ȥ����
���Դ��ڵ�![]() ����Բ
����Բ![]() ����һ��
����һ��![]() ������
������![]() ����
����![]() .
.
�㾦����ֵ���ⳣ���ķ��������֣�
(1)���������֣������ֵ����֤�����ֵ������أ�
(2)ֱ�����������㣬���ڼ��������Ĺ�������ȥ�������Ӷ��õ���ֵ��
�����͡������
��������
22
����Ŀ����֪����![]() �ĵ�����Ϊ
�ĵ�����Ϊ![]() ������
������![]() ����.
����.
��1����![]() ʱ����
ʱ����![]() �����ֵ�����ƶϷ���
�����ֵ�����ƶϷ���![]() �Ƿ���ʵ������
�Ƿ���ʵ������
��2����![]() ������
������![]() �ϵ����ֵΪ-3����
�ϵ����ֵΪ-3����![]() ��ֵ.
��ֵ.
���𰸡�(1)![]() ������
������![]() û��ʵ���⣻(2)
û��ʵ���⣻(2)![]() .
.
�����������������
��1����![]() ʱ��
ʱ��![]() ��
��![]() .��Ϻ����ĵ����Կɵ�
.��Ϻ����ĵ����Կɵ�![]() .
.
���캯��![]() ����
����![]() �����õ������о������ĵ����Կɵ�
�����õ������о������ĵ����Կɵ�![]() ��
��![]() �ϵ�����������
�ϵ�����������![]() �ϵ����ݼ���
�ϵ����ݼ���![]() ���ݴ˿ɵ÷���
���ݴ˿ɵ÷���![]() û��ʵ����.
û��ʵ����.
��2��������ɵ�![]() ��
��![]() ��
��![]() .�ݴ˷��������У�
.�ݴ˷��������У�
����![]() ��
��![]() ��
��![]() ����������
����������![]() ��������.
��������.
����![]() ��
��![]() ��
��![]() ������������
������������![]() ����������
����������![]() .��
.��![]() ���ɵ�
���ɵ�![]() .
.
���Ͽɵ�![]() .
.
���������
��1����![]() ����
����![]() .
.
��![]() ʱ��
ʱ��![]() ��
��![]() .
.
��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() .
.
��![]() ��
��![]() ��������������
��������������![]() ���Ǽ�������
���Ǽ�������![]() .��
.��![]() .
.
����![]() ��
��![]() ����
����![]() ����
����![]() .
.
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() �ϵ�����������
�ϵ�����������![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() �ϵ����ݼ���
�ϵ����ݼ���
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��
���![]() û��ʵ����.
û��ʵ����.
��2����![]() ��
��![]() ����
����![]() .
.
����![]() ����
����![]() ��
��![]() ��
��![]() ������������
������������![]() ��������.
��������.
����![]() ������
������![]()
![]() ����
����![]() ����
����![]()
![]() ����
����![]() .
.
�Ӷ�![]() ��
��![]() ������������
������������![]() ������������
������������![]() .
.
��![]() ����
����![]() ����
����![]() ����
����![]() .
.
��![]() ����
����![]() ����.
����.

 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�