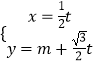题目内容
【题目】设n≥2,n∈N* , 有序数组(a1 , a2 , …,an)经m次变换后得到数组(bm , 1 , bm , 2 , …,bm , n),其中b1 , i=ai+ai+1 , bm , i=bm﹣1 , i+bm﹣1 , i+1(i=1,2,…,n),an+1=a1 , bm﹣1 , n+1=bm﹣1 , 1(m≥2).例如:有序数组(1,2,3)经1次变换后得到数组(1+2,2+3,3+1),即(3,5,4);经第2次变换后得到数组(8,9,7).
(1)若ai=i(i=1,2,…,n),求b3 , 5的值;
(2)求证:bm , i= ![]() ai+jCmj , 其中i=1,2,…,n. (注:i+j=kn+t时,k∈N* , i=1,2,…,n,则ai+j=a1)
ai+jCmj , 其中i=1,2,…,n. (注:i+j=kn+t时,k∈N* , i=1,2,…,n,则ai+j=a1)
【答案】
(1)解:依题意(1,2,3,4,5,6,7,8,…,n),
第一次变换为(3,5,7,9,11,13,15,…,n+1),
第二次变换为(8,12,16,20,24,28,…,n+4),
第三次变换为(20,28,36,44,52,…,n+12),
∴b3,5=52
(2)解:用数学归纳法证明:对m∈N*,bm,i= ![]() ai+jCmj,其中i=1,2,…,n,
ai+jCmj,其中i=1,2,…,n,
(i)当m=1时,b1,i= ![]() ai+jC1j,其中i=1,2,…,n,结论成立,
ai+jC1j,其中i=1,2,…,n,结论成立,
(ii)假设m=k时,k∈N*时,bk,i= ![]() ai+jCkj,其中i=1,2,…,n,
ai+jCkj,其中i=1,2,…,n,
则m=k+1时,bk+1,i=bk,i+bk,i+1= ![]() ai+jCkj+
ai+jCkj+ ![]() ai+j+1Ckj=
ai+j+1Ckj= ![]() ai+jCkj+
ai+jCkj+ ![]() ai+j+1Ckj﹣1,
ai+j+1Ckj﹣1,
=aiCk0+ ![]() ai+j(Ckj+Ckj﹣1)+ai+k+1Ckk,
ai+j(Ckj+Ckj﹣1)+ai+k+1Ckk,
=aiCk+10+ ![]() ai+jCk+1j+ai+k+1Ck+1k+1,
ai+jCk+1j+ai+k+1Ck+1k+1,
= ![]() ai+jCk+1j,
ai+jCk+1j,
所以结论对m=k+1时也成立,
由(i)(ii)可知,对m∈N*,bm,i= ![]() ai+jCmj,其中i=1,2,…,n成立
ai+jCmj,其中i=1,2,…,n成立
【解析】(1)根据新定义,分别进行1次,2次,3次变化,即可求出答案,(2)利用数学归纳法证明即可.