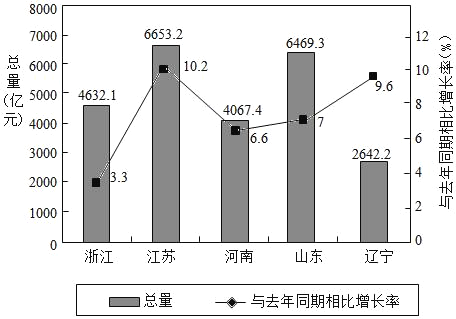
题目内容
【题目】已知椭圆C: ![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
(1)求椭圆C的方程;
(2)是否存在直线l,使得点N平分线段A1B1?若存在,求求出直线l的方程,若不存在,请说明理由.
【答案】
(1)
解:∵椭圆C: ![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,
在椭圆C上,
∴由题意得 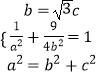 ,解得a2=4,b2=3,
,解得a2=4,b2=3,
∴椭圆C的方程为 ![]() .
.
(2)
解:假设存在这样的直线l:y=kx+m,∴M(0,m),N(﹣ ![]() ,0),
,0),
∵PM=MN,∴P( ![]() ,2m),Q(
,2m),Q( ![]() ),
),
∴直线QM的方程为y=﹣3kx+m,
设A(x1,y1),由 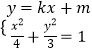 ,得(3+4k2)x2+8kmx+4(m2﹣3)=0,
,得(3+4k2)x2+8kmx+4(m2﹣3)=0,
∴ ![]() ,∴
,∴ ![]() ,
,
设B(x2,y2),由 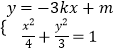 ,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,
,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,
∴x2+ ![]() =
= ![]() ,∴x2=﹣
,∴x2=﹣ ![]() ,
,
∵点N平分线段A1B1,∴ ![]() ,
,
∴﹣ ![]() =﹣
=﹣ ![]() ,∴k=
,∴k= ![]() ,
,
∴P(±2m,2m),∴ ![]() ,解得m=
,解得m= ![]() ,
,
∵|m|= ![]() <b=
<b= ![]() ,∴△>0,符合题意,
,∴△>0,符合题意,
∴直线l的方程为y= ![]()
【解析】(1)由椭圆的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,列出方程组,求出a,b,由此能求出椭圆C的方程.(2)假设存在这样的直线l:y=kx+m,则直线QM的方程为y=﹣3kx+m,由
在椭圆C上,列出方程组,求出a,b,由此能求出椭圆C的方程.(2)假设存在这样的直线l:y=kx+m,则直线QM的方程为y=﹣3kx+m,由 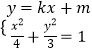 ,得(3+4k2)x2+8kmx+4(m2﹣3)=0,由
,得(3+4k2)x2+8kmx+4(m2﹣3)=0,由 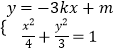 ,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,由此利用根的判别式、韦达定理、中点坐标公式,结合已知条件,能求出直线l的方程.
,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,由此利用根的判别式、韦达定理、中点坐标公式,结合已知条件,能求出直线l的方程.

 阅读快车系列答案
阅读快车系列答案