题目内容
【题目】已知点H(0,﹣8),点P在x轴上,动点F满足PF⊥PH,且PF与y轴交于点Q,Q为线段PF的中点.
(1)求动点F的轨迹E的方程;
(2)点D是直线l:x﹣y﹣2=0上任意一点,过点D作E的两条切线,切点分别为A、B,取线段AB的中点,连接DM交曲线E于点N,求证:直线AB过定点,并求出定点的坐标.
【答案】
(1)解:设F(x,y),∵Q是PF的中点,Q在y轴上,P在x轴上,
∴P(﹣x,0),又H(0,﹣8),∴kPF= ![]() ,kPH=
,kPH= ![]() ,
,
∵PF⊥PH,∴ ![]() ,即x2=4y.
,即x2=4y.
∴动点F的轨迹E的方程x2=4y
(2)解:证明:设直线AB的方程为y=kx+b,
联立方程组 ![]() ,消去y得:x2﹣4kx﹣4b=0,
,消去y得:x2﹣4kx﹣4b=0,
设A(x1,y1),B(x2,y2),则 ![]() ,且△=16k2+16b.
,且△=16k2+16b.
以点A为切点的切线的斜率为kP= ![]() x1,其切线方程为y﹣y1=
x1,其切线方程为y﹣y1= ![]() x1(x﹣x1),
x1(x﹣x1),
即y= ![]() x1x﹣
x1x﹣ ![]() x12,
x12,
同理过点Q的切线的方程为y= ![]() x2x﹣
x2x﹣ ![]() x22,
x22,
联立方程组 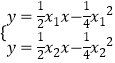 得
得 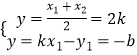 ,
,
即D(2k,﹣b),∵D在直线x﹣y﹣2=0上,
∴2k﹣(﹣b)﹣2=0,即b=2﹣2k,
所以直线AB的方程y=kx+2﹣2k,即y=k(x﹣2)+2,显然该直线恒过定点(2,2).
【解析】(1)设F(x,y),用x,y表示出P点坐标,求出PF、PH的斜率,根据PF⊥PH列方程化简即可;(2)设AB方程为y=kx+b,联立方程组得出A,B坐标的关系,利用导数的几何意义得出切线方程,从而求得D点坐标,得出k,b的关系,即可得出结论.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目